Vanilla PP for Philosophers:
A Primer on Predictive Processing

Wanja Wiese & Thomas Metzinger

The goal of this short chapter, aimed at philosophers, is to provide an overview and brief explanation of some central concepts involved in predictive processing (PP). Even those who consider themselves experts on the topic may find it helpful to see how the central terms are used in this collection. To keep things simple, we will first informally define a set of features important to predictive processing, supplemented by some short explanations and an alphabetic glossary.

The features described here are not shared in all PP accounts. Some may not be necessary for an individual model; others may be contested. Indeed, not even all authors of this collection will accept all of them. To make this transparent, we have encouraged contributors to indicate briefly which of the features are necessary to support the arguments they provide, and which (if any) are incompatible with their account. For the sake of clarity, we provide the complete list here, very roughly ordered by how central we take them to be for “Vanilla PP” (i.e., a formulation of predictive processing that will probably be accepted by most researchers working on this topic). More detailed explanations will be given below. Note that these features do not specify individually necessary and jointly sufficient conditions for the application of the concept of “predictive processing”. All we currently have is a semantic cluster, with perhaps some overlapping sets of jointly sufficient criteria. The framework is still developing, and it is difficult, maybe impossible, to provide theory-neutral explanations of all PP ideas without already introducing strong background assumptions. Nevertheless, at least features 1-7 can be regarded as necessary properties of what is called PP in this volume:

Keywords

Active inference | Attention | Bayesian Inference | Environmental seclusion | Free energy principle | Hierarchical processing | Ideomotor principle | Perception | Perceptual inference | Precision | Prediction | Prediction error minimization | Predictive processing | Predictive control | Statistical estimation | Top-down processing

Acknowledgments

We are extremely grateful to Regina Fabry and Jakob Hohwy for providing very detailed and helpful feedback on a draft of this primer. Thanks also to Lucy Mayne and Robin Wilson for their valuable editorial help. Our student assistant Fabian Martin Römer deserves a special thanks for his professional and reliable help in correcting the formatting of all articles in this collection.

1.Top-down Processing: Computation in the brain crucially involves an interplay between top-down and bottom-up processing, and PP emphasizes the relative weighting of top-down and bottom-up signals in both perception and action.

2.Statistical Estimation: PP involves computing estimates of random variables. Estimates can be regarded as statistical hypotheses which can serve to explain sensory signals.

3.Hierarchical Processing: PP deploys hierarchically organized estimators (which track features at different spatial and temporal scales).

4.Prediction: PP exploits the fact that many of the relevant random variables in the hierarchy are predictive of each other.

5.Prediction Error Minimization (PEM): PP involves computing prediction errors; these prediction error terms have to be weighted by precision estimates, and a central goal of PP is to minimize precision-weighted prediction errors.

6.Bayesian Inference: PP accords with the norms of Bayesian inference: over the long term, prediction error minimization in the hierarchical model will approximate exact Bayesian inference.

7.Predictive Control: PP is action-oriented in the sense that the organism can act to change its sensory input to fit with its predictions and thereby minimize prediction error; among other benefits, this enables the organism to regulate its vital parameters (like levels of blood oxygenation, blood sugar, etc.).

8.Environmental Seclusion: The organism does not have direct access to the states of its environment and body (for a conceptual analysis of “direct perception”, see Snowdon 1992), but infers them (by inferring the hidden causes of interoceptive and exteroceptive sensory signals). Although this is a basic feature of some philosophical accounts of PP (cf. Hohwy 2016; Hohwy 2017), it is controversial (cf. Anderson 2017; Clark 2017; Fabry 2017a; Fabry 2017b).

9.The Ideomotor Principle: There are “ideomotor” estimates; computing them underpins both perception and action, because they encode changes in the world which are registered by perception and can be brought about by action.

10.Attention and Precision: Attention can be described as the process of optimizing precision estimates.

11.Hypothesis-Testing: The computational processes underlying perception, cognition, and action can usefully be described as hypothesis-testing (or the process of accumulating evidence for the internal model). Conceptually, we can distinguish between passive and active hypothesis-testing (and one might try to match active hypothesis-testing with action, and passive hypothesis-testing with perception). It may however turn out that all hypothesis-testing in the brain (if it makes sense to say that) is active hypothesis-testing.

12.The Free Energy Principle: Fundamentally, PP is just a way of minimizing free energy, which on most PP accounts would amount to the long-term average of prediction error.

In the following, we do not assume any familiarity with PP or any mathematical background knowledge, and this introduction will, for the most part, be restricted to the conceptual basics of the PP framework. Having read this primer, one should be able to follow the discussion in the other papers of this collection. However, we would also strongly encourage readers to deepen their understanding of PP by reading (Clark 2016) and (Hohwy 2013), two excellent first philosophical monographs on this topic.

1What Is Predictive Processing? Seven Core Features

Predictive processing (PP) is a framework involving a general computational principle which can be applied to describe perception, action, cognition, and their relationships in a single, conceptually unified manner. It is not directly a theory about the underlying neural processes (it is computational, not neurophysiological), but there are more or less specific proposals of how predictive processing can be implemented by the brain (see, e.g., Engel et al. 2001; Friston 2005; Wacongne et al. 2011; Bastos et al. 2012; Brodski et al. 2015). Moreover, it seems that at least some of the principles which can be applied to descriptions on subpersonal (e.g., computational or neurobiological) levels of analysis can also be applied to descriptions on the personal level (e.g., to agentive phenomena, the structure of reasoning, or phenomenological reports which describe the contents of consciousness). This is one reason why PP is philosophically interesting and relevant. If the theory is on the right track, then:

1.it may provide the means to build new conceptual bridges between theoretical and empirical work on cognition and consciousness,

2.it may reveal unexpected relationships between seemingly disparate phenomena, and

3.it may unify to some extent different theoretical approaches.

But what is PP in the first place? Here is a relatively early formulation of one of its key ideas:1

Wenn die Anschauung sich nach der Beschaffenheit der Gegenstände richten müßte, so sehe ich nicht ein, wie man a priori von ihr etwas wissen könne; richtet sich aber der Gegenstand (als Objekt der Sinne) nach der Beschaffenheit unseres Anschauungsvermögens, so kann ich mir diese Möglichkeit ganz wohl vorstellen. (Kant 1998[1781/87], B XVII)2

One thing Kant emphasizes at this point in the Critique of Pure Reason is that our intuitions (Anschauungen), which constitute the sensory material on which acts of synthesis are performed, are not sense-data that are simply given (cf. Brook 2013, § 3.2). They are not just received, but are also partly shaped by the faculty of intuition (Anschauungsvermögen). In contemporary parlance, the idea can be expressed as follows:

Classical theories of sensory processing view the brain as a passive, stimulus-driven device. By contrast, more recent approaches emphasize the constructive nature of perception, viewing it as an active and highly selective process. Indeed, there is ample evidence that the processing of stimuli is controlled by top-down influences that strongly shape the intrinsic dynamics of thalamocortical networks and constantly create predictions about forthcoming sensory events. (Engel et al. 2001, p. 704)

This is what we here call the first feature of predictive processing: Top-Down Processing. As can be seen, the idea that perception is partly driven by top-down processes is not new (which is not to deny that dominant theories of perception have for a long time marginalized their role). The novel contribution of PP is that it puts an extreme emphasis on this idea, depicting the influence of top-down processing and prior knowledge as a pervasive feature of perception, which is not only present in cases in which the sensory input is noisy or ambiguous, but all the time.3 According to PP, one’s brain constantly forms statistical estimates, which function as representations4 of what is currently out there in the world (feature #2, Statistical Estimation), and these estimates are hierarchically organized (tracking features at different spatial and temporal scales; feature #3, Hierarchical Processing).5 The brain uses these representations to predict current (and future) sensory input and the source of it, which is possible because estimates at different levels of the hierarchy are predictive of each other (feature #4, Prediction). Mismatches between predictions and actual sensory input are not used passively to form percepts, but only to inform updates of representations which have already been created (thereby anticipating, to the extent possible, incoming sensory signals). The goal of these updates is to minimize the prediction error resulting from the prediction (feature #5, Prediction Error Minimization (PEM)), in such a way that updates conform to the norms of Bayesian Inference (feature #6; more on this below). The computational principle of PEM is a general principle to which all processing in the brain conforms (at all levels of the hierarchy posited by PP). From this, it is only a small step towards describing processing in the brain as a controlled online hallucination:6

[A] fruitful way of looking at the human brain, therefore, is as a system which, even in ordinary waking states, constantly hallucinates at the world, as a system that constantly lets its internal autonomous simulational dynamics collide with the ongoing flow of sensory input, vigorously dreaming at the world and thereby generating the content of phenomenal experience. (Metzinger 2004[2003], p. 52)

Note that the contents of phenomenal experience are only part of what is, according to PP, generated through the hierarchically organized process of prediction error minimization (most contents will be unconscious). Summing up the first six core features described above, and adding the seventh feature, we can now give a concise definition of what is called predictive processing in this collection (we will enrich the definition with features 8-12 below):

Predictive Processing (PP) is

• hierarchical predictive coding,
• involving precison-mediated
• prediction error minimization,7
• enabling predictive control.

Note that this definition already goes beyond what is often referred to as predictive coding (especially if predictive coding is just conceived as a computational strategy for data compression, cf. Shi and Sun 1999; Clark 2013a). Firstly, PP is hierarchical. Secondly, precision estimates can fulfil functional roles that go beyond just balancing prior assumptions and current sensory evidence in statistically optimal fashions (see Clark 2013b). Thirdly, PP is often described as action-oriented, in the sense that it enables Predictive Control (feature #7; cf. Seth 2015). This highlights the assumption, held by some, that action is in some sense more important than perception; although perception can be described as a process of gaining knowledge about the world, the main function of gaining this knowledge lies in enabling efficient, context-sensitive action, through which the organism successfully sustains its existence. This becomes evident when PP is considered in the wider context of Friston’s free-energy principle (FEP).8 Before elaborating on this, let us step back and take a look at the problem of perception, viewed from the perspective of predictive coding.

2Predictive Processing and Predictive Coding

As for almost all features of PP (predictive processing), there are also prominent precursors of the PP view on perception. Consider the following statement by Helmholtz:

Die psychischen Thätigkeiten, durch welche wir zu dem Urtheile kommen, dass ein bestimmtes Object von bestimmter Beschaffenheit an einem bestimmten Orte ausser uns vorhanden sei, sind im Allgemeinen nicht bewusste Thätigkeiten, sondern unbewusste. Sie sind in ihrem Resultate einem Schlusse gleich, insofern wir aus der beobachteten Wirkung auf unsere Sinne die Vorstellung von einer Ursache dieser Wirkung gewinnen, während wir in der That direct doch immer nur die Nervenerregungen, also die Wirkungen wahrnehmen können, niemals die äusseren Objecte. (Von Helmholtz 1867, p. 430)9

The problem of perception, as conceived here, has two aspects: (1) percepts are the result of an unconscious inferential process; (2) percepts present us with properties of external objects, although in fact we can only perceive the effects of external objects. A contemporary description of this idea can be found in Dennett’s 2013 monograph, Intuition Pumps and Other Tools for Thinking. He characterizes the curious situation in which the brain finds itself, by likening it to the following fictional scenario:

You are imprisoned in the control room of a giant robot. […] The robot inhabits a dangerous world, with many risks and opportunities. Its future lies in your hands, and so, of course, your own future as well depends on how successful you are in piloting your robot through the world. If it is destroyed, the electricity in this room will go out, there will be no more food in the fridge, and you will die. Good luck! (Dennett 2013, p. 102)

The person inside the robot has only indirect access to the world, via the robot’s sensors, and the effects of executed actions cannot be known but have to be inferred. This illustrates the feature we call Environmental Seclusion (feature #8). Environmental Seclusion is not a computational feature but an epistemological one, yet it appears in descriptions of the problems to which PP computations provide a solution.10 To find out what the different signals received by the robot mean, the person inside has to form a hypothesis about their hidden causes. The problem of inferring the causes of sensory signals is an inverse problem, because it requires inverting the mapping from (external, hidden) causes to (sensory) effects. This is a difficult problem (to say the least), because the same effect could have multiple causes.11 So even if the relationship between causes C and effects E could be described by a deterministic mapping, ƒ: C  E, the inverse mapping, ƒ-1: E  C, would not usually exist. How does the brain solve this problem?

A first observation is that the cause of a sensory effect is underdetermined by the effect, so prior information has to be used to make a good guess about the hidden cause. Furthermore, if we know how the sensory apparatus is affected by external causes, it is easier to infer sensory effects, given information about external causes, than the other way around. So if we have some information about hidden causes, we can form a prediction of their sensory effects. This prediction can be compared to the actual sensory signal, and the extent to which the two differ from each other, i.e., the size of the prediction error gives us a hint as to the quality of our estimate of the hidden cause. We can update this estimate, compute a new prediction, again compare it with current sensory signals, and thereby (hopefully) minimize the prediction error. Ideally, it does not hurt if our first estimate of the hidden cause is really poor, as by constantly computing predictions and prediction errors, and by updating our estimate accordingly, we can become more and more confident that we have found a good representation of the hidden cause.

Let us illustrate this strategy with the following simple example. A teacher enters the classroom and finds a piece of paper on his desk, with the message “The teacher is an impostor. He doesn’t even really exist.” The message has been written with a fountain pen, in blue, which (as the teacher knows) excludes many of his students. To find the culprit, the teacher asks all students using fountain pens with blue ink to come to the front and, using their own pen, to write something on a piece of paper. As it turns out, this involves only three students, A, B, & C, and all use ink of different brands (which makes them distinguishable). The teacher can now form an educated guess about the hidden cause of the message (“The teacher is an impostor. He doesn’t even really exist.”): he assumes that student A is the culprit, and asks A to write down the same message. This can be seen as a prediction of the actual message, and by comparing them the teacher evaluates his guess about its hidden cause. If the ink looks the same there is no prediction error, and the estimate of the hidden cause does not have to be changed — the culprit has been found. If there is a difference, he can update his estimate, by assuming that, say, B has produced the message. By constantly forming predictions (messages written by the suspects) and comparing them with the actual sensory signal (the message on the desk), the teacher eventually minimizes the prediction error and finds the true culprit.

There are a lot of differences between this fictive scenario and the situation in which the brain finds itself. One is that the example involves personal-level agency (just like Dennett’s giant robot thought experiment): the teacher tests the hypothesis that, say, student A is the culprit by asking A to write down a message. Furthermore, the number of possible hidden causes is finite, and the “prediction error” tells the teacher only that a particular student is not implicated. It does not contain any further information about the culprit; it only excludes one of the suspects. The brain cannot go through all possible hypotheses one by one, because there are (potentially) inifinite possible hidden causes in the world. Furthermore, the world is changing, so representations of hidden causes have to be dynamic: adapting to, and anticipating, all (relevant and predictable) changes in the environment. Finally, to be more realistic, the teacher example would have be extended such that the teacher forms predictions about all his sensory inputs all the time. Just as he could infer the causal interactions leading up to the note, he can infer all the causal goings-on around him all the time (including his own influence on the sensory stream).

3Predictive Processing and Bayesian Inference

Bayesian Inference (feature #6) is a computational method to rationally12 combine existing information, about which there is uncertainty, with new evidence. Here, uncertainty means that the information can be described in a probabilistic format, i.e., using a probability distribution. A very simple example would be a situation in which an agent is uncertain which of a finite number of hypotheses is true (as with the teacher above). Uncertainty would then be reflected by the fact that the agent assigns different probabilities to the hypotheses, without assigning a probability of 1 to any of them. But there can also be situations in which the agent’s information is best modeled as being about an infinite number of possibilities (“hypotheses”), for instance, when the agent performs a noisy measurement of a quantity which could have any value in a continuous interval. In such a case, the information can be coded using a probability density function (i.e., a model), which assigns probabilities to regions (e.g., to sub-intervals). The question to which Bayesian inference provides a rational answer (using Bayes’ rule) is the following: how should I update my model when I obtain new information? An example of new information would be information which an agent receives by performing a measurement (assuming the agent already has uncertain information about the quantity to be measured).

Formally, this update involves computing an a posteriori distribution (which is also just called the posterior). The posterior is obtained by combining an a priori distribution (also just called the prior) with a likelihood. The prior codes the information the agent already has; the likelihood codes how the domain about which the agent already has information is related to the domain of the new information obtained. A nice feature of Bayesian inference is that it can reduce uncertainty. Formally, this means that the posterior often has a lower variance — is more precise — than the prior.

Superficially speaking, there is no obvious connection between prediction error minimization (PEM) and Bayesian inference. In fact, it is not obvious why it would even be desirable to implement or approximate Bayesian inference using PEM. Nevertheless, there is one good reason. Recall that the inverse problem of perception is an ill-posed problem: sensory signals, considered as the effects of external events, cannot be mapped to the hidden states of the environment because for every sensory effect there are multiple possible external causes. In other words, there is uncertainty about the hidden causes. Given prior assumptions about these causes, and considering the sensory effects we measure as new evidence, Bayesian inference promises to give us a rational solution to the problem of how we should update our prior assumptions about hidden causes. In other words, what Bayesian inference can give us (at least in principle) is something like a “probabilistic inverse mapping”. This function maps a measured sensory effect to the different (sets of) possible hidden causes, and indicates which possible causes are most likely the actual causes of sensory effects.

But why do we need PEM if we have Bayesian inference? The answer is that Bayesian inference can be computationally complex, even intractable. In simple cases, it is possible to compute the posterior analytically; in other cases, it has to be approximated. In yet other cases, it may be possible to compute the posterior, but what one would really like to have is the maximizer of the posterior (for instance, a single hypothesis that is most likely, after having taken the new evidence into account). Finding the maximizer may again be computationally demanding and can require approximative methods. Some approximative methods involve prediction error minimization. While the motivation for Bayesian inference is independent of prediction error minimization, once Bayesian inference is regarded as a solution to the problem of perception, prediction error minimization can provide a solution to the problem of computing Bayesian updates.

Note that Bayesian inference also works for hierarchical models. Assuming that variables at non-adjacent levels in the hierarchy are conditionally independent, estimates can be updated in parallel at the different levels (cf. Friston 2003, p. 1342), which ideally yields a globally consistent set of estimates (in practice, things are complicated, as Lee and Mumford 2003, p. 1437, point out). Here, the idea is that most objects in the world do not directly influence each other causally, but they are still objects in the same world, which means that causal interactions between two arbitrary objects are usually mediated by other objects. Similarly, different features of a single object are not completely independent, because they are features of the same object, but this does not mean representations of these features must always be jointly processed. For instance, a blue disc can be represented by representing a certain color (blue) at a certain place, and a certain shape (a disc) at the same place. Information about the location of the color gives me information about the location of the shape. If I have a separate representation of the disc’s location, however, I can treat the color and the shape as (conditionally) independent, i.e., given the disc’s location, information about the color does not give me new information about the shape. Computationally, this allows for sparser representations, which may also be reflected by functional segregation in the brain (cf. Friston and Buzsáki 2016, who explore this with a focus on the temporal domain).

4Predictive Processing and the Ideomotor Principle

So far, prediction error minimization has only been described as a way of generating percepts in accordance with sensory input. The primary role of prediction error minimization may not however be to infer hidden causes in the world, but to bring about changes in the world that help the agent stay alive (see section 7 below). Moreover, the primary target for such changes may not be the external but the internal environment of the agent, i.e., its body. In biological systems, organismic integrity is a top-level priority, because a stable organism (which can control its internal states) can survive in different environments, whereas an unstable organism may not survive even in friendly environments. This has been pointed out by Anil Seth:

PP may apply more naturally to interoception (the sense of the internal physiological condition of the body) than to exteroception (the classic senses, which carry signals that originate in the external environment). This is because for an organism it is more important to avoid encountering unexpected interoceptive states than to avoid encountering unexpected exteroceptive states. A level of blood oxygenation or blood sugar that is unexpected is likely to be bad news for an organism, whereas unexpected exteroceptive sensations (like novel visual inputs) are less likely to be harmful and may in some cases be desirable […]. (Seth 2015, p. 9)

Clearly, the goal of interoceptive inference is not simply to infer the internal condition of the body, but to enable predictive control of vital parameters like blood oxygenation or blood sugar (feature #7). Seth provides the following example. When the brain detects a decline in blood sugar through interoceptive inference, the resulting percept (a craving for sugary things) will lead to prediction errors

at hierarchically-higher levels, where predictive models integrate multimodal interoceptive and exteroceptive signals. These models instantiate predictions of temporal sequences of matched exteroceptive and interoceptive inputs, which flow down through the hierarchy. The resulting cascade of prediction errors can then be resolved either through autonomic control, in order to metabolize bodily fat stores (active inference), or through allostatic actions involving the external environment (i.e., finding and eating sugary things). (Seth 2015, p. 10)

Interoceptive prediction error minimization is therefore an illustrative example of how perception and action are coupled, according to PP. A goal of interoceptive PEM is to keep the organism’s vital parameters (such as its blood sugar level etc.) within viable bounds, and this involves both accurately inferring the current state of these parameters and actively changing them (when necessary). Here is how Friston puts it (in terms of minimizing free energy, which under certain assumptions entails minimizing prediction error):

Agents can suppress free energy by changing the two things it depends on: they can change sensory input by acting on the world or they can change their recognition density by changing their internal states. This distinction maps nicely onto action and perception […]. (Friston 2010, p. 129)

In short, the error between sensory signals and predictions of sensory signals (derived from internal estimates) can be minimized by changing internal estimates and by changing sensory signals (through action). What this suggests is that the same internal representations which become active in perception can also be deployed to enable action. This means that there is not only a common data-format, but also that at least some of the representations that underpin perception are numerically identical with representations that underpin action.

This assumption is already present in James’ ideomotor theory (James 1890),13 the core of which is summed up as follows by James: “[T]he idea of the movement M’s sensory effects will have become an immediately antecedent condition to the production of the movement itself.” (James 1890, p. 586; italics omitted). More recently, this has been picked up by common coding accounts of action representation (see Hommel et al. 2001; Hommel 2015; Prinz 1990).14 The basic idea is always similar: The neural representations of hidden causes in the world overlap with the neural underpinnings of action preparation (which means parts of them are numerically identical). In other words, there are “ideomotor” representations, which can function both as percepts and as motor commands.15

Computationally, the Ideomotor Principle (feature #9) exploits a formal duality between action and perception. The duality is this: If I can perceptually access a state of affairs p, this means p has some perceivable consequences (or constituents) c; action is goal-oriented, so by performing an action I want to bring about some state of affairs p. This means action can also be described as a process in which the perceivable consequences c of p are brought about, and perception can be described as the process by which the causes of a hypothetical action (which brings about p, and thereby c) are inferred (for a rigorous description of this idea, see Todorov 2009). The computational benefits of this dual perspective are reaped in the notion of active inference (developed by Friston and colleagues):

In this picture of the brain, neurons represent both cause and consequence: They encode conditional expectations about hidden states in the world causing sensory data, while at the same time causing those states vicariously through action. [...] In short, active inference induces a circular causality that destroys conventional distinctions between sensory (consequence) and motor (cause) representations. This means that optimizing representations corresponds to perception or intention, i.e. forming percepts or intents. (Friston et al. 2011, p. 138) 16

Active inference is often distinguished from perceptual inference. Since both are realized by minimizing prediction error, however, and since their implementations may not be neatly separable, active inference is also used as a more generic term, especially by Friston and colleagues. In the context of the free-energy principle (see below), it denotes the computational processes which minimize free energy and underpin both action and perception: “Active inference — the minimisation of free energy through changing internal states (perception) and sensory states by acting on the world (action).” (Friston et al. 2012a, p. 539).17

Common to both action and perception is (unconscious, approximatively Bayesian) inference. Since neural structures underpinning action and perception, respectively, are assumed to overlap, active and perceptual inference work in tandem.18 This updated and enriched version of the Ideomotor Principle thereby provides a unifying perspective on action and perception, while its deeper implications and challenges are only beginning to be explored.19

5Attention and Precision

One of the many fruitful ideas formulated in the PP framework is that the allocation of attention can be analyzed as the process of optimizing precision estimates (feature #10). This was first put forward by Karl Friston and Klaas Stephan (Friston and Stephan 2007) (two important papers extending this idea are Feldman and Friston 2010 and Hohwy 2012). Since precision estimates function as weightings of prediction error terms, the precision associated with a prediction error influences its impact on processing at other levels. This means that increasing estimated precision can enhance the depth of processing of a stimulus. Furthermore, precision estimates can be changed in a bottom-up and a top-down fashion: Bottom up, precision can be estimated as a function of obtained samples (e.g., as the inverse of the sample variance); top down, precision estimates can be modulated in contexts in which increases or decreases of precision are anticipated, or can function as goal-representations for mental action (Metzinger 2017). The difference between bottom-up and top-down changes in precision estimates can be linked to the difference between endogenous and exogenous attention (for details, see Feldman and Friston 2010 and Hohwy 2012).

Using this precision-optimization account of attention, it is possible to draw a connection between action and attention. Recall that according to the ideomotor principle, some neural structures are part of the neural underpinnings of both action and perception. Assume that neural structure N becomes active when I perceive a person scratching her chin and when I myself am about to scratch my chin. Following Friston et al. (Friston et al. 2011, p. 138), N could function both as a percept and as an intent, though it usually only functions as one of them. So, unless I suffer from echopraxia, perceiving a movement will not usually cause me to move in the same way (although there are situations in which persons do mimic each other to some extent, see Quadt 2017). This can be accounted for within the framework of PP by noting the following: the hypothesis that I am scratching my chin will yield proprioceptive and other sensory predictions (which describe, for example, the states of my muscles when my arm is moving). Unless I am in fact scratching my chin, these predictions will be in conflict with sensory signals, so there will be a large prediction error, which will lead to an update of the hypothesis that I am scratching my chin. In other words, the hypothesis cannot be sustained in the presence of such prediction errors. So to enable movement, precision estimates associated with sensory prediction errors must be cancelled out by top-down modulation. Combining this with the hypothesis that attention increases precision estimates, one could describe this as a process of attending away from somatosensory signals. Conversely, attending to sensory stimuli should impair normal movement (see Limanowski 2017).

This connection between action and attention is also exploited in accounts of self-tickling (see Van Doorn et al. 2014; Van Doorn et al. 2015). Deviances in precision estimates have been linked to attention and motor disorders, and raised in the context of autism and schizophrenia (see Gonzalez-Gadea et al. 2015; Palmer et al. 2015; Van de Cruys et al. 2014; Friston et al. 2014; Adams et al. 2016). This is only one example of how the PP approach may possess great heuristic fecundity and explanatory power for cognitive neuropsychiatry and related fields.

6The Brain as a Hypothesis-Tester

We mentioned above that a person trapped in a giant robot (recall Dennett’s thought experiment) has to form hypotheses about their environment. One reason why PP may seem appealing to some, if dubious to others, is that it applies personal-level descriptions of this kind to the computational level of description (cf. the paper “The hypothesis testing brain”, Hohwy 2010, feature #11). However, such descriptions can at least be heuristically fruitful in trying to answer the question of why we perceive the world the way we do, in particular, the question of what the formal principles of perceptual organization are. Richard Gregory’s classic paper “Perceptions as hypotheses” famously probes the idea that percepts explain sensory signals, and that they have predictive power (Gregory 1980, pp. 182, 186). Helmholtz already suggested an extended version of this idea, namely that movements could be regarded as experiments:

[W]ir beobachten unter fortdauernder eigener Thätigkeit, und gelangen dadurch zur Kenntniss des Bestehens eines gesetzlichen Verhältnisses zwischen unseren Innervationen und dem Präsentwerden der verschiedenen Eindrücke aus dem Kreise der zeitweiligen Präsentabilien. Jede unserer willkührlichen Bewegungen, durch die wir die Erscheinungsweise der Objecte abändern, ist als ein Experiment zu betrachten, durch welches wir prüfen, ob wir das gesetzliche Verhalten der vorliegenden Erscheinung, d.h. ihr vorausgesetztes Bestehen in bestimmter Raumordnung, richtig aufgefasst haben. (Von Helmholtz 1959[1879/1887], p. 39)20

A classical application in the present debate is saccadic eye movements, which are now conceptualized as an embodied form of hypothesis-testing (Friston et al. 2012b). Apart from these heuristic considerations, if PP is on the right track we can ask if the brain literally engages in inference. This question is answered in the affirmative by Alex Kiefer in his contribution to this collection (see Kiefer 2017). A skeptical position is maintained by Jelle Bruineberg (see Bruineberg 2017 and Bruineberg et al. 2016). The more general issue of how folk psychology and PP are related, and to what extent the scientific usage of folk-psychological concepts may need to be revised, is discussed by Joe Dewhurst (see Dewhurst 2017).

7Predictive Processing and Karl Friston’s Free-Energy Principle

Consider the following tautology: Every organism which manages to stay alive for a certain time does not die during that time. Furthermore, staying alive entails running the risk of dying. This is not supposed to be a deep insight into the concept of life, but a seemingly superficial remark about living organisms. It nonetheless has some interesting implications. For every living organism, there are deadly situations which the organism must avoid to stay alive; and perhaps the more sophisticated an organism is, the more potentially deadly situations there are. Just think about the environments in which a bacterium can survive and compare them with those in which a human being can do so. If an organism has managed to stay alive for a certain time, this means it has (thus far) avoided any deadly situations.

If we make a list of possible situations in which an organism could find itself, and compare this list with the possible situations in which the organism is able to survive, we will find two things:

1.for most organisms (e.g., human beings), the second list will be drastically shorter than the first (because there are a lot of deadly situations); and

2.if we observe an organism which is capable of surviving for a decent amount of time, at a random point during its lifetime, it is very likely to be found in a situation from the second list (this echoes the tautology at the beginning of this section).

We can re-express these two observations in a slightly more technical way. Let us call the set of all possible states in which an organism could be its state space, where a state is defined by the current sensory signals received by the organism’s sensory system. In principle, we can now define a probability distribution over this state space which assigns probabilities to the different regions in this space and describes how likely it is to find the organism in the respective regions during its lifetime. Certain regions will have a high probability (e.g., a fish is likely to be found in water); others will have a low probability (a fish is unlikely to be found outside of water). Furthermore, most regions of state space will have a low probability (because there are so many deadly situations). Formally, this means that the entropy of the probability distribution is low (it would be maximal if it assigned probabilities uniformly to the different regions of state space; see below for a simple formal example). With this probability distribution in hand, we can now make a bet on where in its state space the organism will be found, if observed at an arbitrary moment during its lifetime. Since the distribution assigns extremely low probabilities to most regions of state space, we can make a fairly precise guess (e.g., we can guess that a fish will be in water, that a freshwater fish will be in fresh water, and so on).

Now consider the following. Throughout the lifetime of the fish, we take repeated samples of its states and construct an empirical distribution using these samples. An empirical distribution assigns probabilities which reflect the frequency with which samples were (randomly) drawn from the different regions. As a simple example, think of a device which produces one of two numbers, 0 and 1, whenever a button is pushed, and the two numbers are produced with certain probabilities unknown to the agent. It could be that both numbers are produced with the same probability (0.5), or that one is produced much more frequently than the other (say, 0 is produced with probability 0.9, and 1 is produced with probability 0.1). Every time one presses the button, one notes which number has been produced (this is a single sample), and by counting how often each number is produced one can construct an empirical distribution using the relative frequencies. For instance, if 14 out of 100 samples are 0, and the other 86 samples are 1, the empirical distribution could assign the probability 0.14 to 0 and 0.86 to 1. The entropy of this distribution would be approximately 0.58.

But what is entropy in the first place? It is the average surprise of (in this case) the different outputs of the device. Here, surprise (also called “surprisal”) is a technical notion for the negative logarithm of an event’s probability. The average surprise (the entropy) is now computed as follows: H = –[0.14 * log(0.14) + 0.86 * log(0.86)]. If this quantity is low, it is because the surprise values of the individual outcomes are low (or at least most of them). So to have a low entropy, the surprise of states must be low at any time (or at least most of the time).

We can again apply this to the fish example. Most of the time, the fish will be in unsurprising states. Given exhaustive knowledge about the fish, we can in principle describe the regions of the state space in which the fish is likely to be found, and construct an “armchair” probability distribution that reflects this knowledge. Or we can observe the fish and note the relative frequencies with which it is found in different regions of its state space. In the long run, this empirical distribution should become more and more similar to the “armchair” distribution. (This is an informal description of the ergodicity assumption, which is a formally defined feature of certain random processes, see Friston 2009, p. 293.)

So far, we have observed the fish from the outside, from the observer’s perspective. What happens if we change our point of view and observe the fish from “the animal’s perspective” (as Eliasmith 2000, pp. 25 f., calls it)? The key difference is that we do not even know the fish’s current state. An organism gains knowledge about its own current state by sensory measurements, but these measurements provide the organism with only partial and perhaps noisy information. What is more, the organism does not have access to the probability distribution relative to which the surprisal of its states can be computed. Here, the free-energy principle (FEP) provides a principled solution (feature #12).

The general strategy of FEP consists of two steps. The first is to try to match an internally coded probability distribution (a recognition distribution) to the true posterior distribution of the hidden states, given sensory signals. The second is to try to change sensory signals in such a way that the surprise of sensory and hidden states is low at any given time. This may seem to make matters even worse, because now there are two problems: How can the recognition distribution be matched to an unknown posterior, and how can the surprise of sensory signals be minimized, if the distribution relative to which the surprise is defined is unkown? The ingenuity of FEP consists in solving both problems by minimizing free energy. Here, free energy is an information-theoretic quantity, the minimization of which is possible from the animal’s perspective (for details, see Friston 2008; Friston 2009; Friston 2010).

Explaining this requires a slightly more formal description (here, we will simplify matters; a much more detailed, but still accessible, explanation of the free-energy principle can be found in Bogacz 2015). Firstly, “matching” the recognition distribution to an unknown posterior is just an approximation to Bayesian inference in which the recognition distribution is assumed to have a certain form (e.g., Gaussian). This simplifies computations. Secondly, once an approximation to the true model is computed, free energy constitutes a tight bound on the surprisal of sensory signals. Hence, minimizing free energy by changing sensory signals will, implicitly, minimize surprisal.

Note that the connection between FEP and Bayesian inference is straightforward: minimizing free energy entails approximating the posterior distribution by the recognition distribution. If the recognition distribution is assumed to be Gaussian (with the famous bell-shaped probability density function), minimizing free energy entails minimizing precision-weighted prediction errors. So at least under this assumption (which is called the Laplace assumption ), there is also a connection between FEP and prediction error minimization. In fact, FEP can be regarded as the fundamental theory, which can combine the different features of predictive processing described above within a single, formally rigorous framework. However, it is debatable which of these features are actually entailed by FEP. As mentioned before, Environmental Seclusion is an example of a controversial feature (see Fabry 2017a; Clark 2017). Therefore, it could be helpful to look at specific aspects of this novel proposal not only from an empirical, but also from a conceptual and a metatheroetical perspective. This was one major motive behind our initiative, leading to the current collection of texts.

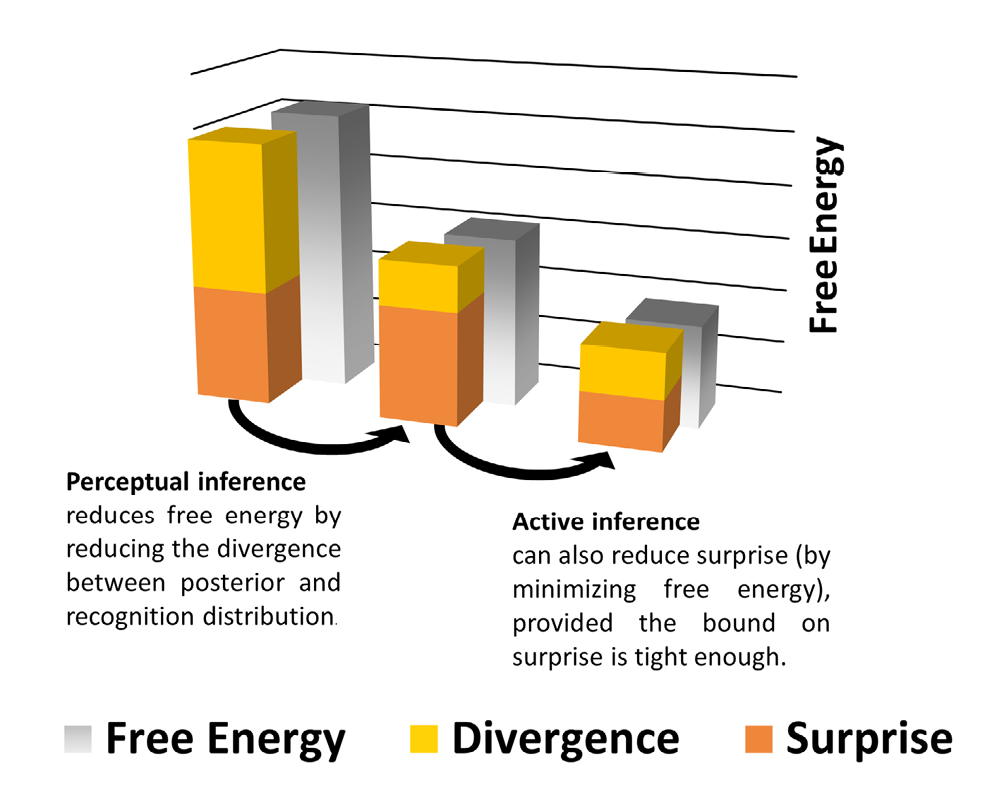
Figure 1: A schematic illustration of how minimizing free energy can, implicitly, minimize surprise. Initially, the recognition distribution will not match the true posterior distribution (of hidden causes, given sensory signals) very well. In order to improve the recognition distribution, it can be changed in such a way that the measured sensory signals become more likely, given this model (this means the model evidence is increased). One way to implement this is by minimizing prediction error. So the assumption is that sensory signals are unsurprising, and this should be reflected by the recognition distribution (i.e., the recognition distribution is altered in such a way that, relative to this distribution, sensory signals are unsurprising). Of course, it could be that the sensory signals are, relative to the true posterior, surprising. For this reason, the recognition distribution has to be tested. This is done, implicitly, by bringing about changes in the world that will, if the recognition distribution is adequate, lead to unsurprising sensory signals. This is active sampling. To some extent, sensory signals will always be surprising, so an adjustment of the recognition distribution will always be required, followed by active sampling, and a further adjustment of the recognition distribution, etc. So this bootstrapping process works through a continuous trial-and-error procedure, and depends on an intimate causal connection between the agent and its environment. Although the black arrows are meant to indicate a temporal sequence, there does not have to be a neat separation between perceptual inference and active inference, and the bootstrapping process could also start with bodily movements.

Glossary

Active inference: 1. Computational process in which prediction error is minimized by acting on the world (“making the world more similar to the model”), as opposed to minimizing prediction error by changing the internal model, i.e. perceptual inference (“making the model more similar to the world”). 2. Also used as a generic term for the computational processes which underpin both action and perception, and, in the context of FEP, for all computational processes that minimize free energy.

Bayesian inference: Updating a model in accordance with Bayes’ rule, i.e. computing the posterior distribution: p(c|s) = p(s|c)p(c)/p(s). For an example, see (Harkness and Keshava 2017).

Counterfactual model: A counterfactual model is a conditional probability distribution that relates possible actions to possible future states (at least following Friston et al. 2012b).

Estimator: A statistical estimator is a function of random variables that are conceived as samples; so an estimator specifies how to compute an estimate from observed data. An estimate is a particular value of an estimator (which is computed when particular samples, i.e., realizations of random variables, have been obtained).

“Explaining Away”: The notion of “explaining away” is ambiguous. 1. Some authors write that sensory signals are explained away by top-down predictions (cf. Clark 2013a, p. 187). 2. Another sense in which the term is used is that competing hypotheses or models are explained away (cf. Hohwy 2010, p. 137). 3. A third sense is as in explaining prediction error away (cf. Clark 2013a, p. 187).

Free energy: In the context of Friston’s FEP, free energy is not a thermodynamic quantity, but an information-theoretic quantity that constitutes an upper bound on surprisal. If this bound is tight, the surprisal of sensory signals can therefore be reduced if free energy is minimized by bringing about changes in the world.

Gaussian distribution: The famous bell-shaped probability distribution (also called the normal distribution). Its prominence is grounded in the central limit theorem, which basically states that many distributions can be approximated by Gaussian distributions.

Generative model: The joint probability distribution of two or more random variables, often given in terms of a prior and a likelihood: p(s,c) = p(s|c)p(c). (Sometimes, only the likelihood p(s|c) is called a “generative model”.) The model is generative in the sense that it models how sensory signals s are generated by hidden causes c. Furthermore, it can be used to generate mock sensory signals, given an estimate of hidden causes.

Hierarchy: PP posits a hierarchy of estimators, which operate at different spatio-temporal timescales (so they track features at different scales). The hierarchy does not necessarily have a top level (but it might have a center — think of the levels as rings on a disc or a sphere).

Inverse problem: From the point of view of predictive coding, the problem of perception requires inverting the mapping from hidden causes to sensory signals. This problem is difficult, to say the least, because there is not usually a unique solution, and sensory signals are typically noisy (which means that the mapping from hidden causes to sensory signals is not deterministic).

Prediction: A prediction is a deterministic function of an estimate, which can be compared to another estimate (the predicted estimate). Predictions are not necessarily about the future (note that a variable can be predictive of another variable if the first carries information about the second, i.e., if there is a correlation, cf. Anderson and Chemero 2013, p. 204). Still, many estimates in PP are also predictive in the temporal sense (cf. Butz 2017; Clark 2013c, p. 236).

Precision: The precision of a random variable is the inverse of its variance. In other words, the greater the average divergence from its mean, the lower the precision of a random variable (and vice versa).

Random variable: A random variable is a measurable function between a probability space and a measurable space. For instance, a six-sided die can be modeled as a random variable, which maps each of six equally likely events to one of the numbers in the set {1,2,3,4,5,6}.

Surprisal: An information-theoretic notion which specifies how unlikely an event is, given a model. More specifically, it refers to the negative logarithm of an event’s probability (also just called “surprise”). It is important not to confuse this subpersonal, information-theoretic concept with the personal-level, phenomenological notion of “surprise”.

References

Adams, R. A., Huys, Q. J. & Roiser, J. P. (2016). Computational psychiatry: Towards a mathematically informed understanding of mental illness. J Neurol Neurosurg Psychiatry, 87 (1), 53-63. https://dx.doi.org/10.1136/jnnp-2015-310737.

Anderson, M. L. (2017). Of Bayes and bullets: An embodied, situated, targeting-based account of predictive processing. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Anderson, M. L. & Chemero, T. (2013). The problem with brain GUTs: Conflation of different senses of ‘’prediction’’ threatens metaphysical disaster. Behavioral and Brain Sciences, 36 (3), 204–205.

Badets, A., Koch, I. & Philipp, A. M. (2014). A review of ideomotor approaches to perception, cognition, action, and language: Advancing a cultural recycling hypothesis. Psychological Research, 80 (1), 1–15. https://dx.doi.org/10.1007/s00426-014-0643-8.

Bastos, A. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries, P. & Friston, K. J. (2012). Canonical microcircuits for predictive coding. Neuron, 76 (4), 695-711. https://dx.doi.org/10.1016/j.neuron.2012.10.038.

Bogacz, R. (2015). A tutorial on the free-energy framework for modelling perception and learning. Journal of Mathematical Psychology. https://dx.doi.org/10.1016/j.jmp.2015.11.003.

Brodski, A., Paasch, G.-F., Helbling, S. & Wibral, M. (2015). The faces of predictive coding. The Journal of Neuroscience, 35 (24), 8997-9006. https://dx.doi.org/10.1523/jneurosci.1529-14.2015.

Brook, A. (2013). Kant’s view of the mind and consciousness of self. In E. N. Zalta (Ed.) The Stanford encyclopedia of philosophy.

Bruineberg, J. (2017). Active inference and the primacy of the ‘I can’. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Bruineberg, J., Kiverstein, J. & Rietveld, E. (2016). The anticipating brain is not a scientist: The free-energy principle from an ecological-enactive perspective. Synthese, 1–28. https://dx.doi.org/10.1007/s11229-016-1239-1.

Burr, C. (2017). Embodied decisions and the predictive brain. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Butz, M. V. (2017). Which structures are out there? Learning predictive compositional concepts based on social sensorimotor explorations. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Clark, A. (2013a). Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behavioral and Brain Sciences, 36 (3), 181–204. https://dx.doi.org/10.1017/S0140525X12000477.

——— (2013b). The many faces of precision (Replies to commentaries on ‘’Whatever next? Neural prediction, situated agents, and the future of cognitive science’’). Frontiers in Psychology, 4, 270. https://dx.doi.org/10.3389/fpsyg.2013.00270.

——— (2013c). Are we predictive engines? Perils, prospects, and the puzzle of the porous perceiver. Behavioral and Brain Sciences, 36 (3), 233–253. https://dx.doi.org/10.1017/S0140525X12002440.

——— (2015). Radical predictive processing. The Southern Journal of Philosophy, 53, 3–27. https://dx.doi.org/10.1111/sjp.12120.

——— (2016). Surfing uncertainty: Prediction, action, and the embodied mind. New York: Oxford University Press.

——— (2017). How to knit your own Markov blanket: Resisting the second law with metamorphic minds. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

——— (in press). Busting out: Predictive brains, embodied minds, and the puzzle of the evidentiary veil. Noûs. https://dx.doi.org/10.1111/nous.12140.

Clowes, M. B. (1969). Pictorial relationships – A syntactic approach. In B. Meltzer & D. Michie (Eds.) (pp. 361–383). Edinburgh, UK: Edinburgh University Press.

Colombo, M. (2017). Social motivation in computational neuroscience: Or if brains are prediction machines then the Humean theory of motivation is false. In J. Kieverstein (Ed.) Routledge handbook of philosophy of the social mind. Abingdon, OX / New York, NY: Routledge.

Dennett, D. C. (2013). Intuition pumps and other tools for thinking. New York, N.Y., and London, UK: W.W. Norton & Company.

Dewhurst, J. (2017). Folk psychology and the Bayesian brain. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Downey, A. (2017). Radical sensorimotor enactivism & predictive processing. Providing a conceptual framework for the scientific study of conscious perception. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Dołega, K. (2017). Moderate predictive processing. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Drayson, Z. (2017). Modularity and the predictive mind. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Egan, F. (2014). How to think about mental content. Philosophical Studies, 170 (1), 115-135. https://dx.doi.org/10.1007/s11098-013-0172-0.

Eliasmith, C. (2000). How neurons mean: A neurocomputational theory of representational content. PhD dissertation, Washington University in St. Louis. Department of Philosophy.

Engel, A. K., Fries, P. & Singer, W. (2001). Dynamic predictions: Oscillations and synchrony in top-down processing. Nat Rev Neurosci, 2 (10), 704–716.

Fabry, R. E. (2017a). Predictive processing and cognitive development. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

——— (2017b). Transcending the evidentiary boundary: Prediction error minimization, embodied interaction, and explanatory pluralism. Philosophical Psychology, 1–20. https://dx.doi.org/10.1080/09515089.2016.1272674.

Feldman, H. & Friston, K. J. (2010). Attention, uncertainty, and free-energy. Frontiers in Human Neuroscience, 4. https://dx.doi.org/10.3389/fnhum.2010.00215.

Friston, K. (2003). Learning and inference in the brain. Neural Networks, 16 (9), 1325–1352.

——— (2005). A theory of cortical responses. Philosophical Transactions of the Royal Society B: Biological Sciences, 360 (1456), 815-836. https://dx.doi.org/10.1098/rstb.2005.1622.

——— (2008). Hierarchical models in the brain. PLoS Computational Biology, 4 (11), e1000211. https://dx.doi.org/10.1371/journal.pcbi.1000211.

——— (2009). The free-energy principle: A rough guide to the brain? Trends in Cognitive Sciences, 13 (7), 293–301. https://dx.doi.org/10.1016/j.tics.2009.04.005.

——— (2010). The free-energy principle: A unified brain theory? Nature Reviews Neuroscience, 11 (2), 127–138. https://dx.doi.org/10.1038/nrn2787.

Friston, K. & Buzsáki, G. (2016). The functional anatomy of time: What and when in the brain. Trends in Cognitive Sciences, 20 (7), 500–511. https://dx.doi.org/10.1016/j.tics.2016.05.001.

Friston, K. & Kiebel, S. (2009). Predictive coding under the free-energy principle. Philosophical Transactions of the Royal Society B: Biological Sciences, 364 (1521), 1211–1221. https://dx.doi.org/10.1098/rstb.2008.0300.

Friston, K. J. & Stephan, K. E. (2007). Free-energy and the brain. Synthese, 159 (3), 417-458. https://dx.doi.org/10.1007/s11229-007-9237-y.

Friston, K., Mattout, J. & Kilner, J. (2011). Action understanding and active inference. Biological Cybernetics, 104 (1-2), 137–160. https://dx.doi.org/10.1007/s00422-011-0424-z.

Friston, K., Samothrakis, S. & Montague, R. (2012a). Active inference and agency: Optimal control without cost functions. Biological Cybernetics, 106 (8), 523-541. https://dx.doi.org/10.1007/s00422-012-0512-8.

Friston, K., Adams, R., Perrinet, L. & Breakspear, M. (2012b). Perceptions as hypotheses: Saccades as experiments. Frontiers in Psychology, 3 (151). https://dx.doi.org/10.3389/fpsyg.2012.00151.

Friston, K. J., Stephan, K. E., Montague, R. & Dolan, R. J. (2014). Computational psychiatry: The brain as a phantastic organ. The Lancet Psychiatry, 1 (2), 148–158. https://dx.doi.org/10.1016/S2215-0366(14)70275-5.

Giordanetti, P., Pozzo, R. & Sgarbi, M. (2012). Kant‘s philosophy of the unconscious. Berlin, Boston: De Gruyter.

Gonzalez-Gadea, M. L., Chennu, S., Bekinschtein, T. A., Rattazzi, A., Beraudi, A., Tripicchio, P., Moyano, B., Soffita, Y., Steinberg, L., Adolfi, F., Sigman, M., Marino, J., Manes, F. & Ibanez, A. (2015). Predictive coding in autism spectrum disorder and attention deficit hyperactivity disorder. Journal of Neurophysiology, 114 (5), 2625-2636. https://dx.doi.org/10.1152/jn.00543.2015.

Gregory, R. L. (1980). Perceptions as hypotheses. Philosophical Transactions of the Royal Society of London. B, Biological Sciences, 290 (1038), 181–197.

Grush, R. (2004). The emulation theory of representation: Motor control, imagery, and perception. Behavioral and Brain Sciences, 27 (3), 377–396.

Gładziejewski, P. (2016). Predictive coding and representationalism. Synthese, 559–582. https://dx.doi.org/10.1007/s11229-015-0762-9.

Harkness, D. L. & Keshava, A. (2017). Moving from the what to the how and where – Bayesian models and predictive processing. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Herbart, J. F. (1825). Psychologie als Wissenschaft neu gegründet auf Erfahrung, Metaphysik und Mathematik. Zweiter, analytischer Teil. Königsberg: Unzer.

Hohwy, J. (2010). The hypothesis testing brain: Some philosophical applications. In W. Christensen, E. Schier & J. Sutton (Eds.) Proceedings of the 9th conference of the Australasian society for cognitive science (pp. 135–144). Macquarie Centre for Cognitive Science. https://dx.doi.org/10.5096/ASCS200922.

——— (2012). Attention and conscious perception in the hypothesis testing brain. Frontiers in Psychology, 3. https://dx.doi.org/10.3389/fpsyg.2012.00096.

——— (2013). The predictive mind. Oxford: Oxford University Press.

——— (2016). The self-evidencing brain. Noûs, 50 (2), 259–285. https://dx.doi.org/10.1111/nous.12062.

——— (2017). How to entrain your evil demon. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Hommel, B. (2015). The theory of event coding (TEC) as embodied-cognition framework. Frontiers in Psychology, 6. https://dx.doi.org/10.3389/fpsyg.2015.01318.

Hommel, B., Müsseler, J., Aschersleben, G. & Prinz, W. (2001). The theory of event coding (TEC): A framework for perception and action planning. Behavioral and Brain Sciences, 24, 849–878. https://dx.doi.org/10.1017/S0140525X01000103.

Horn, B. K. P. (1980). Derivation of invariant scene characteristics from images (pp. 371–376). https://dx.doi.org/10.1145/1500518.1500579.

James, W. (1890). The principles of psychology. New York: Henry Holt.

Kant, I. (1998). Critique of pure reason. Cambridge, MA: Cambridge University Press.

——— (1998[1781/87]). Kritik der reinen Vernunft. Hamburg: Meiner.

Kiefer, A. (2017). Literal perceptual inference. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Lake, B. M., Salakhutdinov, R. & Tenenbaum, J. B. (2015). Human-level concept learning through probabilistic program induction. Science, 350 (6266), 1332-1338. https://dx.doi.org/10.1126/science.aab3050.

Lee, T. S. & Mumford, D. (2003). Hierarchical Bayesian inference in the visual cortex. J. Opt. Soc. Am. A, 20 (7), 1434–1448. https://dx.doi.org/10.1364/JOSAA.20.001434.

Lenoir, T. (2006). Operationalizing Kant: Manifolds, models, and mathematics in Helmholtz’s theories of perception. In M. Friedman & A. Nordmann (Eds.) The Kantian legacy in nineteenth-century science (pp. 141–210). Cambridge, MA: MIT Press.

Limanowski, J. (2017). (Dis-)attending to the body. Action and self-experience in the active inference framework. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Lotze, R. H. (1852). Medicinische Psychologie oder Physiologie der Seele. Leipzig: Weidmann’sche Buchhandlung.

Metzinger, T. (2004[2003]). Being no one: The self-model theory of subjectivity. Cambridge, MA: MIT Press.

——— (2017). The problem of mental action. Predictive control without sensory sheets. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Palmer, C. J., Paton, B., Kirkovski, M., Enticott, P. G. & Hohwy, J. (2015). Context sensitivity in action decreases along the autism spectrum: A predictive processing perspective. Proceedings of the Royal Society of London B: Biological Sciences, 282 (1802). https://dx.doi.org/10.1098/rspb.2014.1557.

Prinz, W. (1990). A common coding approach to perception and action. In O. Neumann & W. Prinz (Eds.) Relationships between perception and action (pp. 167–201). Berlin; Heidelberg: Springer.

Quadt, L. (2017). Action-oriented predictive processing and social cognition. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Seth, A. K. (2015). The cybernetic Bayesian brain: From interoceptive inference to sensorimotor contingencies. In T. Metzinger & J. M. Windt (Eds.) Open MIND. Frankfurt am Main: MIND Group. https://dx.doi.org/10.15502/9783958570108.

Shi, Y. Q. & Sun, H. (1999). Image and video compression for multimedia engineering: fundamentals, algorithms, and standards. Boca Raton, FL: CRC Press.

Sloman, A. (1984). Experiencing omputation: A tribute to Max Clowes. In M. Yazdani (Ed.) New horizons in educational computing (pp. 207–219). Chichester: John Wiley & Sons.

Snowdon, P. (1992). How to interpret ‘direct perception’. In T. Crane (Ed.) The contents of experience (pp. 48–78). Cambridge: Cambridge University Press.

Spratling, M. W. (2016). A review of predictive coding algorithms. Brain and Cognition. https://dx.doi.org/10.1016/j.bandc.2015.11.003.

Stock, A. & Stock, C. (2004). A short history of ideo-motor action. Psychological Research, 68, 176–188. https://dx.doi.org/10.1007/s00426-003-0154-5.

Swanson, L. R. (2016). The predictive processing paradigm has roots in Kant. Frontiers in Systems Neuroscience, 10, 79. https://dx.doi.org/10.3389/fnsys.2016.00079.

Todorov, E. (2009). Parallels between sensory and motor information processing. In M. S. Gazzaniga (Ed.) The cognitive neurosciences. 4th edition (pp. 613–623). Cambridge, MA / London, UK: MIT Press.

Van de Cruys, S., Evers, K., Van der Hallen, R., van Eylen, L., Boets, B., de-Wit, L. & Wagemans, J. (2014). Precise minds in uncertain worlds: Predictive coding in autism. Psychological Review, 121 (4), 649–675. https://dx.doi.org/10.1037/a0037665.

Van Doorn, G., Hohwy, J. & Symmons, M. (2014). Can you tickle yourself if you swap bodies with someone else? Consciousness and Cognition, 23, 1-11. http://dx.doi.org/10.1016/j.concog.2013.10.009.

Van Doorn, G., Paton, B., Howell, J. & Hohwy, J. (2015). Attenuated self-tickle sensation even under trajectory perturbation. Consciousness and Cognition, 36, 147–153. https://dx.doi.org/10.1016/j.concog.2015.06.016.

Von Helmholtz, H. (1855). Ueber das Sehen des Menschen. Leipzig: Leopold Voss.

——— (1867). Handbuch der physiologischen Optik. Leipzig: Leopold Voss.

——— (1959[1879/1887]). Die Tatsachen in der Wahrnehmung. Zählen und Messen. Darmstadt: Wissenschaftliche Buchgesellschaft.

——— (1985[1925]). Helmholtz‘s treatise on physiological optics. Birmingham, AL: Gryphon Editions.

Von Holst, E. & Mittelstaedt, H. (1950). Das Reafferenzprinzip. Die Naturwissenschaften, 37 (20), 464–476.

Wacongne, C., Labyt, E., van Wassenhove, V., Bekinschtein, T., Naccache, L. & Dehaene, S. (2011). Evidence for a hierarchy of predictions and prediction errors in human cortex. Proc Natl Acad Sci U S A, 108 (51), 20754-9. https://dx.doi.org/10.1073/pnas.1117807108.

Wiese, W. (2016). Action is enabled by systematic misrepresentations. Erkenntnis. https://dx.doi.org/10.1007/s10670-016-9867-x.

Zellner, A. (1988). Optimal information processing and Bayes’s theorem. The American Statistician, 42 (4), 278–280. https://dx.doi.org/10.2307/2685143.