Moving from the What to the How and Where – Bayesian Models and Predictive Processing
Dominic L. Harkness & Ashima Keshava
The general question of our paper is concerned with the relationship between Bayesian models of cognition and predictive processing, and whether predictive processing can provide explanatory insight over and above Bayesian models. Bayesian models have been gaining influence in neuroscience and the cognitive sciences since they are able to predict human behavior with high accuracy. Models based on a Bayesian optimal observer are fitted on behavioral data. A good fit is hence interpreted as human subjects “behaving” in a Bayes’ optimal fashion. However, these models are performance-oriented and do not specify which processes could give rise to the observed behavior.
Here, David Marr’s (Marr 1982) levels of analysis can help understand the relationship between performance- and process-oriented models or explanations. Bayesian models are situated at the computational level since they specify what the system (in this case the brain) does and why it does it in this manner. Although Bayesian models can constrain the search space for hypotheses at the algorithmic level, they do not provide a precise solution abouthow a system realizes the observed behavior. Here predictive processing can shed more light on the underlying principles. Predictive processing provides a unifying functional theory of cognition and can thus i) provide an answer at the algorithmic level by answering how the brain realizes cognition, ii) can aid in the interpretation of neurophysiological findings at the implementational level.
Keywords
Bayesian models | Explanation | Marr | Predictive processing | Unification
Recent findings indicate that the human brain can be seen as a Bayesian inference machine (Knill and Pouget 2004). This is motivated by the fact that the brain faces the so-called inverse problem: the brain cannot gain access to the world outside of the skull by itself, and must rely on the sensory organs to make sense of the world. This sensory input is oftentimes noisy, and furthermore, a many-to-many relationship holds between external causes and perceived sensory effects. As a consequence, the brain must infer the causes of sensory input from these effects.
Bayesian models of cognition create ideal observer models of cognitive phenomena and use them as a backdrop to which human performance is compared (Colombo and Seriés 2012). What these models have shown is that humans often behave in a Bayes’ optimal fashion and therefore the behavior itself can be accurately predicted (Ernst and Banks 2002). Bayesian models can thus be seen as performance-oriented, since it is solely the behavior of the ideal observer that is compared to the behavior of human subjects. However, this paper will argue that this does not suffice if one wants to reach an explanation of human cognition.
What is additionally needed are process-oriented models that can describe which functional or physical components are involved in giving rise to human behavior as well as the causal relations that hold between these components. We will argue in this paper that Bayesian models of cognition alone do not provide such insight. Instead, we propose that predictive processing (Clark 2013; Hohwy 2013) can provide a process-oriented theory that can give an account of how Bayesian inference is realized by the brain. Furthermore, unlike Bayesian models, predictive processing can serve as a so-called mechanism sketch, thus being able to guide researchers in finding mechanistic explanations of a target cognitive phenomenon. To exemplify how Bayesian models relate to predictive processing we turn to David Marr’s (Marr 1982) three level account of explanations. The paper is structured as follows: first we will describe Bayesian models and predictive processing and follow with an introduction to David Marr’s levels. Finally we will compare Bayesian models and predictive processing in light of Marr’s levels of analysis.
2Bayesian Models
One of the central problems in the cognitive sciences is how the brain builds rich and generalized models of the world given sparse and noisy sensory data. In this regard, Bayesian models have become an increasingly popular tool in the understanding of cognition. They have been used to model, amongst others, visual perception (Yuille and Kersten 2006), inductive learning and human reasoning (Tenenbaum et al. 2006), motor planning (Körding and Wolpert 2006), or multisensory integration (Ernst and Banks 2002). In this section, we will explore the basis of Bayesian modeling, taking the problem of multisensory cue integration as an example.
One of the attractions of the Bayesian approach is its simplicity of formulation. The three core tenets of the modeling scheme are: the task of the organism, prior knowledge of the environment and the knowledge of the way the environment is sensed by the organism (Kersten et al. 2004). These three basic components can then be used to model and further predict an organism’s behavior.
This approach can be realized with Bayes’ rule. For instance, if we have a set of hypotheses H and want to test the probability of a given hypothesis h within this set. Before obtaining evidence, we assume that this hypothesis h has a probability, P(h), which is the prior probability. We can then observe certain data d given this hypothesis which brings us to P(d|h) which is the likelihood of observing this data. Using Bayes’ rule we can then update the probability of the hypothesis given the data, i.e. P(h|d), which is the posterior probability of h given the data d. The remaining term P(d) is the marginal probability of d, i.e. the sum of the joint probabilities over the hypothesis space H. Simply put:
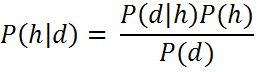
The problem of how the brain integrates different sensory signals to form a coherent picture of the world is one that is of great importance, and has been approached by Bayesian modelling techniques extensively. Bayesian models of multisensory integration have thus far shown that humans are close to Bayes’ optimal when integrating sensory signals of different modalities, i.e. human performance closely fits the predictions made by these models (Ernst and Banks 2002; Körding and Wolpert 2004; Triesch et al. 2002). In a similar vein, Shams et al. (Shams et al. 2005) showed that visual and auditory signals are integrated or segregated depending on the stimulus condition in a Bayesian fashion and thus gave a computational account of the phenomenon of sound-induced flash illusion (Shams et al. 2000; Shams et al. 2002). They investigated this by presenting subjects with a varying number of light flashes on the screen with a simultaneously varying number of sound beeps in each trial and having them report the perceived number of flashes and beeps. When one flash was presented with one beep, the signals ‘appear’ to originate from the same source. Whereas, when one light flash is coincident with four sound beeps, the two signals are perceived to originate from different sources and are, hence, considered separate events. If a single flash is accompanied by two beeps, the single flash is often perceived as two flashes and the flashes and beeps are perceived to originate from the same source. Based on this paradigm, Shams et al. (Shams et al. 2005) developed an ideal observer model that would account for bimodal sensory signal segregation, partial integration and complete integration. Human behavioral data was then compared with the ideal observer model.
The Bayesian model (ideal observer model) was developed with the assumption that auditory signal (A) and visual signal (V) are statistically independent as noise processes that corrupt these signals are independent. It is also assumed that A and V are caused by separate sources ZA and ZV respectively. Thus, information about the likelihood of signal A occurring given a source ZA is given by the probability distribution P(A|ZA) Similarly, P(V|ZV) represents the likelihood of sensory signal V given a source ZV. The distribution P(ZA|ZV) denotes the observer’s prior knowledge about auditory and visual events in the environment. As Shams et al. mention, “the priors may reflect hard-wired biases imposed by the physiology and anatomy of the brain, [...] as well as biases imposed by the task, the observer’s state, etc.” (Shams et al. 2005, p. 1924). Given the auditory and visual signals, an ideal observer would try to best estimate the sources ZA and ZV, which can be represented as a posterior probability distribution P(ZA, ZV|A, V). By applying Bayes’ rule, the following results:

Shams et al. (Shams et al. 2005) approximated the priors from the observed data by marginalizing the joint probability across all combinations of A and V. To do this, data from half of the participants was used to estimate the priors and the rest of the data was used to test the model’s predictive accuracy:
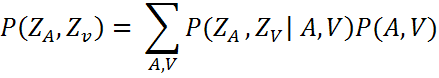
Results suggested that human observer’s performance were consistent with the ideal observer’s. The observed human behavioral data fitted well with the model predictions for conditions in which signals from the two modalities were integrated and segregated. Hence, it was shown that “the brain uses a mechanism similar to Bayesian inference [...] as a statistically optimal computational strategy” (Shams et al. 2005, p. 1927) to integrate signals from different modalities.
It must be mentioned here that the example taken above deviates from traditional models of Bayesian cue integration (Beierholm et al. 2007), that assume a single signal source location that gives rise to latent variables belonging to different modalities e.g. a visual and an auditory. In these cases the source is determined using the maximum likelihood estimation method. This is done by taking the inverse of the variances of the visual and the auditory signal and representing them as precisions of the visual and auditory signal.
As seen above, Bayesian models specify when a behavioral response to a given stimulus can be regarded as rational or optimal according to Bayes’ rule. However, since Bayesian models are performance-oriented they do not give an account of how this Bayesian optimality is achieved in the brain, either functionally or physically. They do not inform us about the underlying causal structure that leads to the human behavior predicted by Bayesian models. One hypothesis that does aim at giving a process-oriented theory in the realm of the Bayesian brain hypothesis (Knill and Pouget 2004) is called predictive processing (PP) (Clark 2013; Clark 2016) or prediction error minimization (PEM) (Hohwy 2013).
3Predictive Processing
Picture the brain as a black box that cannot directly access the world outside of the skull. The only means it has to gain such access consists of utilizing the sensory information that is provided to the brain via the sensory organs. For example, the eyes provide the brain with visual sensory information. As a consequence, the brain does not have access to the external causes that lead to the sensory input. Thus the brain is in the business of having to infer the causes of sensory input from its effects. This has been coined the inverse problem. The question then is how is the sensory input used to gain any knowledge about the hidden external causes that lead to that sensory input?
The general assumption is that the information that is provided by the sensory organs will always contain a certain amount of uncertainty due to noise or other factors that may distort the sensory signal. Also, one cause may have many different effects and the opposite is also possible, that many causes can have the same effect. Taking an example from Hohwy (Hohwy 2013), an actual bicycle, a bicycle poster, or even a bee swarm that coincidentally flew in a formation that resembles a bicycle might all give rise to the same visual percept. How then could the brain discern between these different possibilities? For one it could assess the probability of each possibility, e.g. how probable is it that the bicycle-like visual image being perceived is actually a swarm of bees? Then, depending on the context, different hypotheses are more likely. For example, if a person perceives a bicycle-like visual input in front of a train station, the priors of the different hypotheses will not be equal from the start. The bee hypothesis seems unlikely in any case, since bees do not usually fly in bicycle-like formations. The poster hypothesis seems unlikely as well, since people generally do not park bicycle posters in front of a train station. Yet, bicycle posters do exist and are thus still more likely than the bee hypothesis. The most likely hypothesis seems to be that the visual information represents an actual bicycle.
How then can the brain assess how likely any of these hypotheses are? Why will humans, even if the sensory information could be the same in all three cases, i.e. different causes leading to identical effects, nonetheless perceive an actual bicycle in most cases?
Here, we must appreciate that sensory inputs contain statistical regularities. These regularities are captured in so-called generative models — models that aim at representing the causal structure of the world in a probabilistic format (every time I clap my hands a sound occurs) and are continuously updated in light of the evidence. One of predictive processing’s core tenets is that these models are updated and new information is integrated according to Bayes’ rule. With the help of these generative models, the brain can then attempt at predicting what the next sensory input might be given the last sensory input. For example, if a face that is lit from the top turns to the left, the brain can persistently predict how the lighting on the face will change since these lighting effects are also subject to statistical regularities that have been perceived in the past.
We now have two values that can be continuously compared with one another: the actual sensory input and the predicted sensory input which is dependent on previous observations about some facet of the world. To solve the inverse problem and thereby infer external causes from their effects, predictive processing argues that the brain is a system that constantly compares predicted with actual sensory input and tries to minimize the discrepancy between these two values up to expected levels of noise, i.e. to minimize prediction errors. The reasoning behind this is that the less prediction error occurs, the better the model fits the sensory input, and a model that has a good fit accurately represents the causal structure of the world. However, prediction errors will occur in every case due to the noise in sensory input. In the case of high prediction error, the brain can reduce these prediction errors in two ways. Either it can change its generative models according to the sensory input. This can be seen as learning (or perceptual inference), since the models are updated in light of new sensory information to further refine the models and ultimately achieve a more accurate representation of the external causes that lead to that sensory input. Alternatively, it can change the sensory input to match the predictions deriving from the models. This would then be action, or more formally active inference (Friston et al. 2009). Referring back to the bicycle example from above, by moving closer to the seen bicycle-like visual image, the agent could more accurately discern different hypotheses. Yet, what determines which path is chosen to reduce the amount of prediction error?
As mentioned before, sensory input always contains a varying amount of noise. To deal with this, the brain must “take [this] variability [...] into consideration — it needs to assess the precision of the prediction error.” (Hohwy 2012, p. 4). In other words, since sensory information can contain different amounts of noise, the brain must be able to determine whether a given sensory input can be regarded as ‘trustworthy’, i.e. does this sensory information provide precise information about the external causes or should the brain rather rely on its models? It is then the precision of prediction errors (Hesselmann et al. 2010) that determines whether models are updated in light of new evidence or the agent engages in active inference to match the sensory input to its expected states. If noise in sensory input is low, prediction errors are amplified, since they are precise and model revisions can ensue. If noise is high, the resulting prediction errors are deemed imprecise and lead to an amplification of predictions (ibid., p. 1). Just as there are generative models about external causes that lead to the effects observed by the sensory organs, there are also models about precisions. Since noise in sensory input is context-sensitive and may vary between sensory modalities and the environmental setting (for example that precision declines on foggy days in the visual domain), it is necessary for the brain to have these precision estimates (Hohwy 2012; Friston and Stephan 2007; Feldman and Friston 2010) in order to better minimize prediction errors.
The optimization of these precision estimates have been identified with attention (Feldman and Friston 2010; Hohwy 2012), arguing that it may serve as “a gating or gain mechanism that somehow optimizes sensory processing.” (Hohwy 2012, p. 6). Thus, by attending to a certain feature of the sensory input the precision can be increased and consequently the amount of prediction error minimized in a more efficient fashion.
Another crucial feature of predictive processing is that prediction errors are minimized across a cortical hierarchy spanning over numerous levels (Friston 2005; Mumford 1991). Each of these levels is concerned with different properties of the sensory input and contains generative models about these properties. Thus, any level attempts to predict the next state of the level below. Furthermore, as one goes down the hierarchy, the temporal grain at which predictions are made increases and sensory properties are more variant. For example, predictions in V1 must be able to process fast-changing properties of the visual input. As one goes up the hierarchy, the processed properties become more invariant and the temporal scale increases, as for example in temporal cortex. This allows “the brain to build up representations of environmental causes from basic stimulus attributes to more and more abstract and invariant properties.” (Hohwy 2010, p. 136). As a consequence, “each cortical area is an expert for inferring certain aspects of the visual scene” (Lee and Mumford 2003, p. 1436) and this can actually be seen if one looks at the functional segregation between cortical areas. For example, V1 processes basic sensory properties, such as orientation or location, of the visual input via simple and complex cells (Hubel and Wiesel 1968), V4 has been associated with processing form and structure (Desimone and Schein 1987) and area MT with motion perception (Maunsell and Essen 1983).
The hierarchical structure of predictive processing implies that the major portion of processing proceeds top-down, since predictions are passed down from higher to lower levels. Bottom-up messages on the other hand then only carry the prediction errors to the levels above for further processing.
As a short summary, predictive processing argues that the brain only has access to its own states due to its ‘black-box’ status. It uses sensory information provided by the sensory organs to create generative models that capture the causal structure of the world (inferring from effects to causes). These generative models are in turn used to predict the brain’s next state. If the predictions match the sensory input well, a good model has been selected, since it accurately represents the world and consequently is perceived. However, if a discrepancy between the predicted and actual sensory input arises, meaning a high amount of prediction error occurs that exceeds the expected levels of noise, the system (the brain) will either engage in active inference or change its models according to the sensory input. The factors that determine which option is pursued are the precision of the prediction errors and the respective priors. High precision prediction errors lead to model revisions, since the sensory input is regarded as trustworthy. Low precision on the other hand leads to action, the aim being to adjust sensory input according to the model.
4Marr’s Levels
Having presented both Bayesian models and predictive processing, the question arises how these two frameworks relate to each other. Here, David Marr’s (Marr 1982) levels of analysis can help.
4.1Levels of Analysis
Marr (Marr 1982) proposed that any cognitive system needs to be analyzed at three different levels in order to fully explain it. These are the computational, algorithmic, and implementational levels and each level should answer certain questions about the investigated system (p. 23f). At the computational level the what and why questions are answered, i.e. what does the system do and why does it do it? Thus, specifying an optimal behavioral output to a certain perceptual input and stating why this output is optimal would be located at the computational level. The algorithmic level answers how the system accomplishes what it does by concentrating on the underlying processes that lead to the investigated behavior of the system in question. Yet, theories at the algorithmic level need not specify where or how physically the system is realized. These questions are answered at the implementational level, i.e. where in the brain is the system localized and how is the system physically realized?
Although these levels seem to provide a straightforward approach to investigating a cognitive system, the relationship between levels remains unclear. The relation between the levels of analysis is one of realization, meaning what are the processes that lead to the observed behavior and how are these processes realized by a physical system. Also, Marr advocated that the three levels should be seen as formally independent of one another, i.e. that many algorithms could realize the computational problem and the algorithms could be realized by many different physical parts. However, this formal independence “does not entail that the algorithms used by the human cognitive system are best discovered independently of a detailed understanding of its neurobiological mechanisms.” (Colombo and Seriés 2012, p. 17, original emphasis).
We argue that the minimal requirement for an algorithmic-level theory consists in making causal claims about the structure of the system, and for an implementational-level theory that its proposed components of the system are structurally describable. Computational-level theories do not and need not meet either of these requirements. For a computational-level model it suffices to specify an output to some input. Often, these input-output relations have a mathematical formulation. Yet, as Marr (Marr 1982) has proposed, all levels should be considered if one wants to reach a full explanation of any cognitive system. The alternative is so-called single-level theorizing, which leads to incomplete explanations for several reasons. For example, remaining at the computational level results in such theories being largely “under-constrained and somewhat arbitrary” (Love 2015, p. 233) since the behavior observed and described by computational-level theories could be inconsistent with results from e.g. cognitive psychology or neuroscience (Griffiths et al. 2012, p. 264; Colombo and Seriés 2012). If there are no physical counterparts that can compute what a certain computational-level model presupposes it seems to make little sense to further pursue that particular model.1 Likewise, remaining at the implementational level may result in having descriptions about the neural hardware, reaction times, or neural networks, yet still being unable to incorporate these insights into higher-order cognitive systems or concepts (Cooper and Peebles 2015). For example, how do neural firing rates inform us about emotions or problem-solving tasks? Such bottom-up driven theories appear unguided by an overarching question and “do no more than mimic in an unenlightening way.” (Marr 1982, p. 347, in Cooper and Peebles 2015, p. 2).
Our intuition behind this paper is nicely captured by Kaplan & Craver (Kaplan and Craver 2011) who state that “the line that demarcates explanations from merely empirically adequate models seems to correspond to whether the model describes the relevant causal structures that produce, underlie, or maintain the explanandum phenomenon” (p. 602). In the case of computational-level theories or models, insight into the causal structure of the system cannot be gained. This is due to the fact that these types of theories or models are performance-oriented, i.e. they aim at specifying an output given some input while “no internal structure is specified within the model” (Colombo and Seriés 2012, p. 10). Algorithmic — as well as implementational-level theories on the other hand are regarded as process-oriented theories since they provide insights into the causal processes that realize the abstract computational problem. Again, the aim of the algorithmic and implementational level is to give an account of how and where the computational problem is computed/solved.
4.2Marr’s Levels, Bayesian Models and Predictive Processing
It is widely agreed upon that Bayesian models are located at the computational level since “[t]hey help researchers understand what a cognitive system does, because they describe and predict its behavior.” (Zednik and Jäkel 2014, p. 666, emphasis added) and “attempt to explain why cognition produces the patterns of behavior that [it] does.” (Jones and Love 2011, p. 170). To what extent computational-level theories such as Bayesian models can inform and offer constraints at the algorithmic and implementational level is currently being debated in light of the Bayesian program (Zednik and Jäkel 2014; Zednik and Jäkel 2016; Colombo and Hartmann 2015; Bowers and Davis 2012). Zednik & Jäkel (Zednik and Jäkel 2016) for example argue that Bayesian models can constrain theories at the algorithmic level by reverse-engineering from the computational level to the levels below via a number of heuristics. In this paper we will not dive into the details of this discussion since it suffices for our argument that Bayesian models do exhibit the tendency to remain at the computational level and that “mechanism is neglected in favor of a focus on behavior.” (Love 2015, p. 233).2 Bayesian models do not provide sufficient explanations for cognitive systems and provide little insight into the causal structure of the investigated system (algorithmic) nor the physical entities that constitute that system (implementational) by themselves. This poses a problem for so-called top-down approaches that aim at proceeding from the computational level downwards to the algorithmic and implementational levels (Love 2015) as it remains unclear “whether a given probabilistic model is inconsistent with particular cognitive or neural processes.” (Griffiths et al. 2012, p. 264).
Predictive processing on the other hand can be considered an algorithmic level theory since it provides an account of how cognition may be realized. It’s very ambitious in its scope and argues that cognition adheres to one core principle: the minimization of prediction error. It divides a system such as the brain into different subcomponents and provides a theory of how these subcomponents interact with one another. Here predictive processing has been criticized since up to this point the concepts employed are purely functional. They do not make any reference to neurobiological structures in the brain (Rasmussen and Eliasmith 2013).
Yet, there is mounting empirical evidence in favor of this theory. Consequently, as evidence accumulates and physical properties are identified that could realize the functional properties proposed by predictive processing, predictive processing can incrementally be regarded as an implementational theory. This means identifying physical structures that could realize e.g. prediction errors, precision, or how the cortical hierarchy is structured. In fact, some of these concepts have already been identified with neurophysiological entities that can be structurally described. In the remainder of this paper we will present four such cases.
One of the most important aspects of predictive processing is that the brain is structured hierarchically. This entails the distinction between feedforward (prediction errors) and feedback (predictions) connections. Predictive processing then gains ‘implementational weight’ once these connections, so far only described functionally, are associated with entities in the brain that can be identified and structurally described. This has been done. It has been hypothesized that the two mentioned types of connections are realized by pyramidal cells in the brain. In particular, feedforward connections are associated with superficial pyramidal cells, and feedback connections with deep pyramidal cells (Mumford 1991; DeFelipe et al. 2002; Friston 2005). Since these types of cells can be e.g. measured and analyzed, and are able to pass on messages as supposed by predictive processing, they seem to be ideal candidates to count as realizers of the structural hierarchy.
The next example concerns how precision could be realized in the brain. Friston et al. (Friston et al. 2012) argue that the realization of precision may consist in the modulation of the synaptic signal-to-noise ratio via synaptic gain. The proposed structural entity responsible for this mechanism is the neurotransmitter dopamine. Since dopamine is involved in many different cognitive functions, and a unifying theory regarding the function of dopamine is still lacking, this approach “provides a novel perspective on the role of dopamine that accounts for its apparently diverse roles in terms of a single mechanism”. (ibid., p. 2).
Another strong indication for predictive processing comes from Hosoya et al. (Hosoya et al. 2005) who state that retinal ganglion cells encode changes in the visual field to which an organism (here salamanders and rabbits) has adapted to rather than the raw visual image. Spike trains from ganglion cells in the retinae of salamanders and rabbits were recorded and the visual field was manipulated so that the subject was adapted to that particular environment and then a novel/uncorrelated stimulus was used to probe the ganglion cells’ receptive fields. It was seen that the response of the ganglion cells flattened (reduced) once it was adapted to a particular environment while they became more sensitive to novel stimuli. This systematic effect of enhancing sensitivity to novel stimuli and relative to the adapting environment gives a strong suggestion towards a strategy of dynamic predictive coding (Rao and Ballard 1999).
Lastly, predictive processing can also aid in the interpretation of extra-classical field effects. If two neighboring neurons have the same orientation preference and a visual stimulus extends over the boundaries of the receptive field of one of these neurons, the response of that particular neuron will be suppressed. This type of effect has been found in a number of brain areas (V1, V2, V4, MT; (Allman and Miezin 1985)) and been termed as extra-classical receptive field effects. Here, Rao & Ballard (Rao and Ballard 1999) argue that “visual cortical neurons with extra-classical [receptive field] properties can be interpreted as residual error detectors, signaling the difference between an input signal and its statistical prediction based on an efficient internal model of natural images.” (Rao and Ballard 1999, p. 79).
Our main argument then consists in the following: by taking evidence from both the computational level (provided by Bayesian models) and implementational level (provided by neurophysiological findings) into consideration, one may, albeit provocatively, conclude that the algorithmic level (predictive processing) can be regarded as the best candidate to form the bridge between behavior and the brain (Love 2015). This means that Bayesian models increase the evidence in favor of predictive processing at the computational level and neurophysiological findings at the implementational level.
By considering how Bayesian models, predictive processing and implementational findings relate to each other in the Marrian framework we can assess how each of them contribute to understanding cognition as a whole. Bayesian models provide no (or at least very little) insight into the causal structure of a system. Implementational level findings on the other hand give accurate physical descriptions of a system’s components and their interactions, but fail to provide an over-arching theory about how these single components or processes result in a large-scale system such as the brain. Lastly, predictive processing gives an algorithmic level account of how cognition is functionally realized. As mentioned in the previous paragraphs, predictive processing then seems to be an ideal candidate to bind computational level theories with implementational findings due to being an algorithmic level theory.
5Conclusion
According to the Marrian framework, to reach a full explanation of a target system one must investigate and understand that system at all three levels of analysis. At the computational level we have Bayesian models, that accurately predict human behavior and give strong reasons to interpret the brain as a Bayesian inference machine. However, due to their focus on performance rather than the underlying processes, Bayesian models lack insight into the physical components that lead to the observed human behavior, and the causal relations that hold between them. Yet, this does not mean that they do not contribute to the scientific enterprise of understanding human cognition. They do provide strong evidence that human behavior approximates Bayesian optimality (in line with predictive processing).
Next we have implementational findings provided by the neurosciences that investigate and describe physical structures in the brain. Yet, taken by themselves, they provide little insight into how a complex system, such as the brain, could realize the multitude of behaviors that it does. More importantly, explaining how implementational-level findings lead to the observed behaviors at the computational level seems almost impossible.
Our main argument then states that predictive processing, as an algorithmic-level theory, is an ideal candidate to tie computational-level findings with implementational-level ones together. Bayesian models confirm predictive processing’s premise that humans do in fact approximate Bayes’ optimal behavior. Predictive processing then provides a functional theory of how such behavior comes about. Lastly, once implementational-level findings are identified that can physically realize the functions proposed by predictive processing, we reach an increasingly detailed account of mind and brain.
References
Allman, J. & Miezin, F. (1985). Stimulus specific responses from beyond the classical receptive field: Neurophysiological mechanisms for local-global comparisons in visual neurons. Annual Review of Neuroscience. https://dx.doi.org/10.1146/annurev.ne.08.030185.002203.
Beierholm, U., Shams, L., Ma, W. J. & Koerding, K. (2007). Comparing Bayesian models for multisensory cue combination without mandatory integration (pp. 81–88).
Bowers, J. S. & Davis, C. J. (2012). Bayesian just-so stories in psychology and neuroscience. Psychol Bull, 138 (3), 389-414. https://dx.doi.org/10.1037/a0026450.
Clark, A. (2013). Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behavioral and Brain Sciences.
——— (2016). Surfing uncertainty: Prediction, action, and the embodied mind. New York: Oxford University Press.
Colombo, M. & Hartmann, S. (2015). Bayesian cognitive science, unification, and explanation. axv036. https://dx.doi.org/10.1093/bjps/axv036.
Colombo, M. & Seriés, P. (2012). Bayes in the brain—on Bayesian modelling in neuroscience. 63 (3), 697-723. https://dx.doi.org/10.1093/bjps/axr043.
Cooper, R. P. & Peebles, D. (2015). Beyond single-level accounts: The role of cognitive architectures in cognitive scientific explanation. Top Cogn Sci, 7 (2), 243-58. https://dx.doi.org/10.1111/tops.12132.
Craver, C. F. (2007). Explaining the brain. Mechanisms and the mosaic unity of neuroscience. Oxford: Oxford University Press.
DeFelipe, J., Alonso-Nanclares, L. & Arellano, J. I. (2002). Microstructure of the neocortex: Comparative aspects. Journal of Neurocytology.
Desimone, R. & Schein, S. J. (1987). Visual properties of neurons in area V4 of the macaque: Sensitivity to stimulus form. Journal of Neurophysiology.
Ernst, M. O. & Banks, M. S. (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature. https://dx.doi.org/10.1038/415429a.
Feldman, H. & Friston, K. (2010). Attention, uncertainty, and free-energy. Frontiers in Human Neuroscience, 4, 215.
Friston, K. (2005). A theory of cortical responses. Philosophical Transactions of the Royal Society B: Biological Sciences, 360 (1456), 815-836. https://dx.doi.org/10.1098/rstb.2005.1622.
Friston, K. J. & Stephan, K. E. (2007). Free-energy and the brain. 159 (3), 417-458.
Friston, K. J., Daunizeau, J. & Kiebel, S. J. (2009). Reinforcement learning or active inference? 4 (7). https://dx.doi.org/10.1371/journal.pone.0006421.
Friston, K. J., Shiner, T., FitzGerald, T., Galea, J. M., Adams, R., Brown, H., Dolan, R. J., Moran, R., Stephan, K. & Bestmann, S. (2012). Dopamine, affordance and active inference. PLoS Computational Biology, 8 (1), e1002327. https://dx.doi.org/10.1371/journal.pcbi.1002327.
Griffiths, T. L., Vul, E. & Sanborn, A. N. (2012). Bridging levels of analysis for probabilistic models of cognition. Current Directions in Psychological Science, 21 (4), 263-268. https://dx.doi.org/10.1177/0963721412447619.
Hesselmann, G., Sadaghiani, S., Friston, K. J. & Kleinschmidt, A. (2010). Predictive coding or evidence accumulation? False inference and neuronal fluctuations. PLoS ONE, 5 (3), e9926. https://dx.doi.org/10.1371/journal.pone.0009926.
Hohwy, J. (2010). The hypothesis testing brain: Some philosophical applications. In W. Christensen, E. Schier & J. Sutton (Eds.) Proceedings of the 9th conference of the Australasian society for cognitive science (pp. 135–144). Macquarie Centre for Cognitive Science. https://dx.doi.org/10.5096/ASCS200922.
——— (2012). Attention and conscious perception in the hypothesis testing brain. Front Psychol, 3, 96. https://dx.doi.org/10.3389/fpsyg.2012.00096.
——— (2013). The predictive mind.
Hosoya, T., Baccus, S. A. & Meister, M. (2005). Dynamic predictive coding by the retina. Nature, 436 (7047), 71-77. https://dx.doi.org/10.1038/nature03689.
Hubel, D. H. & Wiesel, T. N. (1968). Receptive fields and functional architecture of monkey striate cortex. The Journal of Physiology, 195 (1), 215-243.
Jones, M. & Love, B. C. (2011). Bayesian fundamentalism or enlightenment? On the explanatory status and theoretical contributions of Bayesian models of cognition. Behavioral and Brain Sciences, 34 (4), 169. https://dx.doi.org/10.1017/S0140525X10003134.
Kaplan, D. & Craver, C. F. (2011). The explanatory force of dynamical and mathematical models in neuroscience: A mechanistic perspective. Philosophy of Science, 78 (4), 601-627. https://dx.doi.org/10.1086/661755.
Kersten, D., Mamassian, P. & Yuille, A. (2004). Object perception as Bayesian inference. Annu. Rev. Psychol., 55, 271–304.
Knill, D. C. & Pouget, A. (2004). The Bayesian brain: The role of uncertainty in neural coding and computation. Trends in Neurosciences, 27 (12). https://dx.doi.org/10.1016/j.tins.2004.10.007.
Körding, K. P. & Wolpert, D. M. (2004). Bayesian integration in sensorimotor learning. Nature, 427 (6971), 244–247.
——— (2006). Bayesian decision theory in sensorimotor control. Trends in Cognitive Sciences, 10 (7), 319–326.
Lee, T. S. & Mumford, D. (2003). Hierarchical Bayesian inference in the visual cortex. Optical Society of America, 20 (7), 1434.
Love, B. C. (2015). The algorithmic level is the bridge between computation and brain. Topics in Cognitive Science, 7 (2), 230-242. https://dx.doi.org/10.1111/tops.12131.
Marr, D. (1982). Vision: A computational approach. San Francisco: Freeman.
Maunsell, J. H. & Essen, V. D. C. (1983). Functional properties of neurons in middle temporal visual area of the macaque monkey. I. Selectivity for stimulus direction, speed, and orientation. Journal of Neurophysiology.
Mumford, D. (1991). On the computational architecture of the neocortex. Biological Cybernetics, 65 (2), 135-145. https://dx.doi.org/10.1007/BF00202389.
Rao, R. P. N. & Ballard, D. H. (1999). Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat Neurosci, 2 (1), 79-87. https://dx.doi.org/10.1038/4580.
Rasmussen, D. & Eliasmith, C. (2013). God, the devil, and the details: Fleshing out the predictive processing framework. Behavioral and Brain Sciences. https://dx.doi.org/10.1017/S0140525X12002154.
Shams, L., Kamitani, Y. & Shimojo, S. (2000). Illusions: What you see is what you hear. Nature.
——— (2002). Visual illusion induced by sound. Cognitive Brain Research.
Shams, L., Ma, W. J. & Beierholm, U. (2005). Sound-induced flash illusion as an optimal percept. Neuroreport, 16 (17), 1923–1927.
Tenenbaum, J. B., Griffiths, T.L. & Kemp, C. (2006). Theory-based Bayesian models of inductive learning and reasoning. Trends in Cognitive Sciences.
Triesch, J., Ballard, D. H. & Jacobs, R. A. (2002). Fast temporal dynamics of visual cue integration. Perception, 31 (4), 421–434.
Yuille, A. & Kersten, D. (2006). Vision as Bayesian inference: Analysis by synthesis? Trends Cogn. Sci. (Regul. Ed.), 10 (7), 301-8. https://dx.doi.org/10.1016/j.tics.2006.05.002.
Zednik, C. & Jäkel, F. (2014). How does Bayesian reverse-engineering work? In P. Bello, M. Guarini, M. McShane & B. Scassellati (Eds.) Proceedings of the 36th annual conference of the cognitive science society (pp. 666–671). Austin, TX: Cognitive Science Society.
——— (2016). Bayesian reverse-engineering considered as a research strategy for cognitive science. Synthese. https://dx.doi.org/10.1007/s11229-016-1180-3.
1 This is only the case when one is interested in the human brain and human cognition, not some artificial system that may achieve human-like behavior, yet is composed of different parts/hardware.
2 Mechanisms (Craver 2007; Bechtel1994) are located at the algorithmic and implementational levels.