Meeting in the Dark Room: Bayesian Rational Analysis and Hierarchical Predictive Coding

Sascha Benjamin Fink & Carlos Zednik

At least two distinct modeling frameworks contribute to the view that mind and brain are Bayesian: Bayesian Rational Analysis (BRA) and Hierarchical Predictive Coding (HPC). What is the relative contribution of each, and how exactly do they relate? In order to answer this question, we compare the way in which these two modeling frameworks address different levels of analysis within Marr’s tripartite conception of explanation in cognitive science. Whereas BRA answers questions at the computational level only, many HPC-theorists answer questions at the computational, algorithmic, and implementational levels simultaneously. Given that all three levels of analysis need to be addressed in order to explain a behavioral or cognitive phenomenon, HPC seems to deliver more complete explanations. Nevertheless, BRA is well-suited for providing a solution to the dark room problem, a major theoretical obstacle for HPC. A combination of the two approaches also combines the benefits of an embodied-externalistic approach to resolving the dark room problem with the idea of a persisting evidentiary border beyond which matters are out of cognitive reach. For this reason, the development of explanations spanning all three Marrian levels within the general Bayesian approach may require combining the BRA and HPC modeling frameworks.

Keywords

Bayesian rational analysis | Dark room problem | Embodiment | Hierarchical predictive coding | Levels of analysis | Modeling frameworks

1Introduction

Two methodologically distinct modeling frameworks contribute to the rising prominence of the view that the mind and brain are Bayesian. On the one hand, Bayesian Rational Analysis (BRA) is used in cognitive psychology to characterize behavioral and cognitive phenomena as forms of optimal probabilistic inference (Anderson 1991; Griffiths et al. 2008; Oaksford 2001; Oaksford and Chater 2007). On the other hand, Hierarchical Predictive Coding (HPC) is used in theoretical neuroscience to model information processing in the brain (Clark 2013; Friston 2010; Hohwy 2013; Rao and Ballard 1999). Although both of these modeling frameworks are grounded in the formal tools and concepts of Bayesian statistics, they differ with respect to their explanatory scope.1 In particular, they address different levels of analysis in David Marr’s tripartite conception of explanation in cognitive science (Marr 1982).

As is well-known, Marr argued that in order to “completely understand” the visual system, it must be analyzed at three distinct levels. Marr’s levels can be distinguished according to the different types of questions investigators are likely to ask about a particular cognitive system (see also McClamrock 1991). The computational level is characterized by questions about what the system is doing, and why it is doing it. Questions of this kind can be answered by specifying mathematical functions that describe the system’s behavior, and by determining the extent to which these functions reflect relevant structures in the environment (Shagrir 2010). In contrast, the algorithmic level of analysis concerns questions about how the system does what it does—questions that can be answered by specifying the individual steps of an algorithm for computing or approximating the mathematical function that describes the system’s behavior. Finally, at the implementational level of analysis, questions are asked about where in the brain the relevant algorithms are actually realized, by identifying individual steps of the relevant algorithm with the activity of particular physical structures in the brain (Zednik 2017).

Ever since Marr applied this three-level scheme to the phenomenon of visual perception, it has served as a backdrop for comparing and evaluating the explanatory scope of modeling frameworks in cognitive science quite generally. Therefore, the first aim of the present discussion is to highlight the differences between the BRA and HPC modeling frameworks by illuminating them against this backdrop. Specifically, it will be argued that whereas the BRA framework answers what- and why-questions and therefore speaks directly to Marr’s computational level, it is neutral concerning the algorithmic and implementational levels of analysis. In contrast, proponents of HPC are keen to address all three levels of analysis simultaneously (see also Harkness and Keshava 2017).

The second aim is to explore the relationship between the BRA and HPC modeling frameworks, and to suggest that even though HPC is broader in scope and might therefore be thought to supplant BRA, they in fact complement each other in mutually beneficial ways. On the one hand, HPC puts paid to the allegation that the general Bayesian approach “eschews mechanism altogether” (Jones and Love 2011, p.173), because it answers questions at the algorithmic and implementational levels of analysis in addition to the computational level. On the other hand, as we will show, BRA helps to address concerns related to the dark room problem (Clark 2013; Mumford 1992; Sims 2017), which has been thought to undermine the explanatory credentials of HPC. Additionally, a combination of the two approaches marries the benefits of an embodied-externalistic approach to resolving the dark room problem with the idea of a persisting evidentiary border. Because they complement one another in these ways, a combination of the Bayesian Rational Analysis and Hierarchical Predictive Coding modeling frameworks offers a promising avenue to full-fledged Bayesian explanations in cognitive science.

2Bayesian Rational Analysis and the Computational Level

Bayesian approaches in cognitive science are motivated by the insight, often attributed to Hermann von Helmholtz, that many kinds of behavior and cognition can be viewed as solutions to problems of inference under uncertainty (von Helmholtz 1867). For example, perception can be viewed as a solution to the problem of inferring the cause of a particular sensation (“Was it a bird?”), and motor action might be viewed as a solution to the problem of selecting an adequate course of action (“Should I try to catch it?”). In line with Helmholtz’ insight, the aim of BRA is to formally characterize a cognitive system’s behavior as an optimal solution to a particular probabilistic inference task in the environment (Anderson 1991; Griffiths et al. 2008; Oaksford 2001; Oaksford and Chater 2007). To this end, proponents of BRA specify the probabilistic inference tasks in which cognitive systems appear to be engaged, formally characterize the environment in which these tasks are solved, and derive optimal solutions to those tasks according to the rules of probability theory, most notably among them Bayes’ rule:

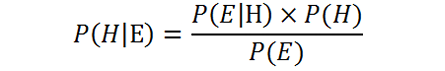
We can consider the left side of this equation to be a formalization of Helmholtz’ insight: P(H|E) is the posterior probability of some hypothesis H (e.g. “It was a bird”), given evidence E that may speak either for or against it (e.g. “I saw a yellow beak”). The right side prescribes that the posterior probability should depend on the prior probability P(H) that the hypothesis is true independent of the evidence (e.g. the probability of encountering birds in a given environment), as well as on the likelihood P(E|H) that evidence E will be available if H is in fact true (e.g. the salience of beaks) and the probability of encountering evidence E independent of the truth of H. Notably, because natural environments are unpredictable and complex, real-world inference typically involves considering not just the probability of a single hypothesis, but rather considering a distribution of probabilities over a space of competing hypotheses. Indeed, many different things could have caused the relevant sensation (e.g. a bird, a plane, Superman), and many different behavioral actions could be performed (e.g. catching, but also running, screaming, laughing maniacally).

The optimal solutions derived using Bayes’ rule closely approximate the behavioral data in a wide variety of behavioral and cognitive domains. Phenomena as varied as perceptual cue-combination (Ernst and Banks 2002), memory and categorization (Anderson 1991), judgment and decision making (Griffiths and Tenenbaum 2006), sensorimotor learning (Körding and Wolpert 2004), reasoning (Oaksford 2001), and language learning (Xu and Tenenbaum 2007) can all be viewed as forms of optimal probabilistic inference in an uncertain environment.2 But what exactly is the explanatory import of this finding? The characterization of behavior and cognition as a form of optimal probabilistic inference allows investigators to answer questions at Marr’s computational level of analysis (Jones and Love 2011; Oaksford 2001; Oaksford and Chater 2007; Zednik and Jäkel 2016; Harkness and Keshava 2017; cf. Bowers and Davis 2012). Specifically, it allows them to answer questions about what a cognitive system is doing, and why. In general, whereas an answer to a what-question is delivered by describing a system’s behavior, an answer to a why-question is delivered by demonstrating this behavior’s “appropriateness” with respect to the “task at hand” (Marr 1982: 24; see also: Shagrir 2010). BRA delivers on both counts. Regarding questions about what a system is doing, whenever an optimal solution is closely approximated by the behavioral data, the former provides an empirically adequate description of the latter. As for questions about why a system does what it does, there is a clear sense in which the system can be thought to behave as it does because that way of behaving is optimal in the sense prescribed by probability theory.3

The fact that BRA is purpose-built for answering what- and why-questions at the computational level distinguishes it from many other modeling frameworks in cognitive science. Traditional frameworks such as classical computationalism and connectionism are designed to answer questions at the algorithmic level of analysis about how the relevant system does what it does, and to a lesser extent, questions at the implementational level about where in the brain the relevant structures and processes are located. Put differently, whereas BRA is mostly concerned with describing behavioral and cognitive phenomena as well as with assessing their appropriateness with respect to some particular task environment, most other modeling frameworks in cognitive science are designed to describe the component parts, operations, and organization of the mechanisms responsible for these phenomena (Bechtel and Richardson 1993; Piccinini and Craver 2011). Because BRA remains neutral with respect to the algorithmic and implementational levels, however, it has been accused of “eschew[ing] mechanism altogether” (Jones and Love 2011, p.173).

To what extent is BRA’s focus on the computational level and simultaneous neglect of mechanisms a virtue rather than a vice? Insofar as the computational level of analysis—and in particular, the answering of why-questions—remains somewhat underappreciated (Marr 1982; Shagrir 2010), BRA is poised to make an important explanatory contribution: By providing formal answers to questions about what a cognitive system is doing, proponents of this modeling framework can attain a heightened understanding of the nature of cognition and behavior itself, including its mathematical structure. As for why-questions, BRA may be poised to contribute to our understanding of a particular behavior’s teleology and role in a containing environment (Griffiths et al. 2012; Oaksford and Chater 2007)—despite the fact that questions remain about how teleological considerations factor into explanation in cognitive science (Zednik 2017; cf. Danks 2008).

That said, in line with Marr’s three-level account, it would be a mistake to think that answering what- and why-questions is sufficient for the purposes of explaining a behavioral or cognitive phenomenon. To wit, Jones and Love have recently argued that:

[I]t would be a serious overreaction simply to discard everything below the computational level. As in nearly every other science, understanding how the subject of study (i.e., the brain) operates is critical to explaining and predicting its behavior [… M]echanistic explanations tend to be better suited for prediction of new phenomena, as opposed to post hoc explanation. [...] Much can be learned from consideration of how the brain handles the computational challenge of guiding behavior efficiently. (Jones and Love 2011, p. 177)

In other words, the explanatory success of the general Bayesian approach arguably depends on the extent to which the computational-level insights delivered by BRA can be supplemented with insights into behavioral and cognitive mechanisms at the algorithmic and implementation levels of analysis.4

Unfortunately, there is considerable disagreement about how best to supplement the BRA modeling framework so as to address questions at levels below the computational. Some investigators—most notably proponents of the so-called Bayesian coding hypothesis (Knill and Pouget 2004; Ma et al. 2006)—have sought to identify probability distributions and Bayes’ rule with specific physical structures and processes in the brain. However, it would be a mistake to think that the answers BRA provides at the computational level impose significant constraints on the answers that may be given to questions at the algorithmic and implementational levels. As Marr himself has previously argued, “there is a wide choice available at each level, and the explication of each level involves issues that are rather independent of the other two” (Marr 1982, p. 25). Indeed, although the Bayesian coding hypothesis may yet be confirmed, the ability to describe behavior and cognition as a form of optimal probabilistic inference at the computational level does not require or even imply that the brain actually invokes Bayes’ rule to compute over probability distributions (Colombo and Series 2012; Maloney and Mamassian 2009). Perhaps for this reason, an increasing number of investigators instead co-opt techniques from machine learning and artificial intelligence to develop biologically plausible algorithms that approximate optimal probabilistic inference without directly implementing either Bayes’ rule or probabilistic representations (e.g. Griffiths et al. 2015; Sanborn et al. 2010, cf. Kwisthout and van Rooij 2013). However, there exist a great number of options, and few principled guidelines for how to choose between them (see Zednik and Jäkel 2016 for discussion). In general, therefore, despite the fact that the BRA modeling framework is useful for answering what- and why-questions at the computational level, it remains unclear how to proceed so as to develop full-fledged scientific explanations that span all three of Marr’s levels.

3Hierarchical Predictive Coding: Complement or Alternative?

Although there may be many different ways in which to supplement the computational-level insights provided by BRA, it is worth considering one particularly prominent candidate: Hierarchical Predictive Coding (HPC). HPC-theorists have developed a wide range of algorithms that exhibit a common computational architecture: a hierarchy of processing stages, where each higher stage is tasked with predicting the state of the preceding stage, and where each lower stage forwards an error signal—a measure of a prediction’s accuracy—to the higher stage.5 At every stage in this hierarchy, Bayes’ rule is used (or approximated) to combine past predictions with error signals so as to result in the construction of increasingly veridical representations of the world. Although these representations are typically used to infer the causes of perceptual stimuli (Rao and Ballard 1999), proponents of the HPC modeling framework have also argued that cognitive systems often “bring the world in line” by “seeking or generating the sensory consequences that they (or rather, their brains) expect” (Clark 2013, p. 186; see also: Friston 2005).

Whereas the BRA modeling framework can be used to formally characterize perception and action as forms of optimal probabilistic inference, HPC is used to develop algorithms that actually perform this kind of inference. That is, the algorithms developed within the HPC modeling framework can be viewed as potential answers to questions about how a particular cognitive system does what it does, i.e. as descriptions of the functional processes that contribute to that system’s behavior. Although much work has yet to be done to determine which (if any) of these algorithms actually constitute a correct answer—i.e. a true description of functional processes in our brains—the fact that answers to how-questions are being developed is often considered the central explanatory contribution of HPC (e.g., Spratling 2013).

Although the focus may be on the algorithmic level of analysis, many HPC-theorists also make it a point to address questions at the implementational level that ask where in the brain the relevant algorithms might be realized. To this end, they identify the particular steps of an HPC-algorithm, or elements of the general HPC-architecture, with particular neuronal structures or processes (e.g. Bastos et al. 2012). For example, the claim that perception and action depend on the propagation of predictions and error signals has motivated the search for specific neural pathways along which this two-way propagation could take place. In particular, Friston (Friston 2005, p. 829) proposes to identify such pathways in “functionally distinct subpopulations [of neurons]”. He suggests the deep pyramidal cells as the locus of error propagation, and the superficial pyramidal cells as pathways for transmitting expectations (see also: Friston 2009). In this way, in addition to answering how-questions at the algorithmic level of analysis, proponents of HPC also often seek to answer where-questions at the implementational level.

Insofar as HPC promotes the formulation of testable claims about the algorithms that are used to perform optimal probabilistic inference, and about the neural structures in which these algorithms are implemented, HPC and BRA might be thought to complement one another. Clark appears to suggest as much when he argues that:

[T]he hierarchical and bidirectional predictive processing story, if correct, would rather directly underwrite the claim that the nervous system approximates, using tractable computational strategies, a genuine version of Bayesian inference. The computational framework of hierarchical predictive processing realizes, using the signature mix of top-down and bottom-up processing, a robustly Bayesian inferential strategy, and there is mounting neural and behavioral evidence [...] that such a mechanism is somehow implemented in the brain. (Clark 2013, p. 189)

That said, although Clark espouses the idea that human and animal cognizers may in fact perform optimal probabilistic inference—the central claim of BRA—it is worth noting that he does not explicitly endorse the methods of BRA. Indeed, it is fair to question whether these methods provide explanatory insights that go beyond the ones delivered by HPC. Although answers to what- and why-questions at the computational level may not impose significant constraints on the algorithmic and implementational levels, the opposite may still be true. Algorithms always produce a particular output that can be measured or described. Therefore, an understanding of how a cognitive system does what it does should allow investigators to understand what that system is actually doing. Indeed, the algorithms used in the HPC modeling framework are known to compute or approximate optimal solutions to problems of probabilistic inference under uncertainty (Rao and Ballard 1999; Friston 2010). Thus, HPC-theorists agree with proponents of BRA that cognitive systems optimally solve probabilistic inference tasks in their environments, but they arrive at this conclusion indirectly, via the algorithmic level, rather than directly, by considering the computational level itself. In this sense, the generic answer to what-questions given by proponents of BRA is implicit in the answers given to how-questions by proponents of HPC.

In addition to answering what-questions, the HPC modeling framework also answers questions about why. Many HPC-theorists argue that cognitive systems behave as they do because that way of behaving leads to the minimization of prediction error (e.g. Clark 2013; Friston 2009; Friston 2010). At first glance, this may seem to differ from the generic way of answering why-questions in the BRA modeling framework, which appeals to the claim that cognitive systems behave as they do because that way of behaving is optimal with respect to the relevant task environment. Indeed, whereas HPC answers why-questions by looking at features internal to a particular system—the algorithms being deployed—BRA answers these questions by considering external features, namely the statistical structure of environment in which that system is situated. Still, HPC’s answers to why-questions entail the answers developed in BRA: prediction error will be minimized whenever Bayes’ rule is applied to update representations of the external world, and whenever cognitive systems act so as to “bring the world in line”. By minimizing prediction error in either one of these two ways, the system’s behavior inevitably approaches optimality in the sense prescribed by probability theory. Therefore, like the answers to what-questions, the answers to why-questions developed within the BRA modeling framework are in fact entailed by the answers developed in HPC.

In summary, although the HPC modeling framework is most clearly directed at the algorithmic and implementational levels of analysis, it is also well-suited for answering questions at the computational level. Perhaps for this reason, while BRA is plagued by the accusation that it “eschews mechanism” (Jones and Love 2011), HPC-theorists regularly present their approach as a unifying framework that is capable of simultaneously addressing all three levels of analysis (e.g. Clark 2013; Hohwy 2013). In this sense, the explanatory scope of HPC exceeds the scope of BRA. Not only that, the scope of HPC appears to fully subsume the scope of BRA. Because the answers given to computational-level questions by proponents of HPC entail the answers that would also be given by advocates of BRA, it is unclear what BRA’s own unique contribution actually is. Does HPC render BRA superfluous?

4Meeting in the Dark Room

BRA can contribute to a unified Bayesian conception of the mind in several ways. We will mainly focus on how the methods and practices of BRA are poised to solve one of HPC’s most pernicious puzzles, the dark room problem (Mumford 1992; Sims 2017; see also the commentary on Clark 2013). But, in passing, we will address how BRA provides us with additional interpretational tools to understand behavior, and how BRA complements HPC-explanations such that we may distinguish how-possibly from how-actually explanations. If BRA contributes in these ways, then although HPC exceeds BRA in explanatory scope and subsumes its answers to what- and why-questions, there are reasons to believe that the development of satisfying three-level explanations involves a combination of resources from both modeling frameworks.

Recall that, from the perspective of HPC, a cognizer behaves as it does in order to minimize prediction error. It can do so either by adjusting its represented predictions about what happens in the environment so that they better fit the incoming sensory data, or by acting in order to make the world match its predictions. Minimization of prediction error therefore can come in both directions of mind-world-fit. In the fleeting, dynamic world which we inhabit, however, one particularly easy way to ensure this kind of fit is to seek an evenly heated, silent, dark place which deprives the system of any sensory stimulation whatsoever, and to predict that nothing about this place will change. In such a “dark room”, the error for predicting that everything will stay the same is minimized—because ex hypothesi, nothing ever changes. Therefore, seeking such a dark room would appear to be a cognizer’s best strategy for prediction-error minimization. Evidently, however, there is a mismatch between this strategy and the ways in which biological cognizers actually behave: In the real world, we avoid such dark rooms for much of our lives. HPC seems unable to explain why cognizers are found playing bridge in living rooms, chasing mates in noisy clubs, listening in lecture halls, navigating the woods and busy market streets, and so on. The erratic nature of such dynamic, complex, and chaotic environments increases the chance that predictions will fail. Still, we prefer them over dark rooms. The fact that real-world cognizers are regularly found in dynamic, unpredictable environments challenges the adequacy of the generic HPC-answer to why-questions: cognitive systems do what they do because it minimizes prediction error. The best strategy for doing just that—going into the dark room—appears to be widely ignored.6

Can HPC-theorists explain why cognitive systems avoid dark rooms, and instead behave in far more interesting ways? Several HPC-theorists have tried to explain why certain features of our cognitive architecture lead us to avoid dark rooms. For example, Andy Clark argues:

[C]hange, motion, exploration, and search are themselves valuable for creatures living in worlds where resources are unevenly spread and new threats and opportunities continuously arise. This means that change, motion, exploration, and search themselves become predicted. (Clark 2013, p. 193)

Hohwy similarly argues that predictions about surprisal rates of an internalized model—so called “hyper-priors”—are what keep us out of dark rooms:

[W]e don’t end up in dark rooms. We end up in just the range of situations we are expected to end up in on average. It is true we minimize prediction error and in this sense get rid of surprise. But this happens against the background of models of the world that do not predict high surprisal states, such as the prediction that we chronically inhabit a dark room. (Hohwy 2013, p. 87)

Finally, Schwartenbeck et al. 2013 strike a similar chord when they analyze exploration as a comparison between two different models the agent has of itself: the agent predicts that it will perform diverse actions in the future, compares these predictions to the actions it is currently performing, and if there is a mismatch, acts in order to minimize the prediction error.

On each one of these responses, dark rooms are avoided because the sensory stimuli encountered in such rooms diverge from the predicted stimuli. Notably, saying that change, motion, exploration, search, future acts and surprisal states themselves become predicted is tantamount to saying that they are internally represented at some level of the hierarchy. Thus, responses of this type can be thought to be internalistic: It is an internal feature of the system that contributes to the avoidance of dark rooms. As such, this response is well in line with HPC’s focus on the algorithmic level: it seems easy to encode such a prediction as, for example, a prior probability at a particular level of the processing hierarchy. But there is reason to be unsatisfied with any internalistic response insofar as the likelihood of these internalistic predictions themselves can be adjusted. It is accurate that going into a dark room would increase prediction error on the level where change, motion, exploration, etc. are predicted, but it would seem to simultaneously decrease prediction error on lower levels of the hierarchy which are closer to the sensorimotor periphery: whenever a cognizer is situated in the dark room, predicting that everything will remain dark produces no error at these lower levels. Thus, a question remains: at which hierarchical level should prediction error be minimized?

As long as both predictions about sensory input and surprisal rates etc. are malleable, no answer follows by necessity. Should the higher level predictions change so as to fit the incoming sensory data in a dark room? Or should the higher level predictions remain fixed, so that the system moves away from the dark room so as to bring the incoming sensory information in line with the higher level prediction? The internalist’s answer would be: act in such a way that the error for higher-level predictions is minimized. But an equally adequate strategy would seem to be: lower the precision estimates associated with these predictions while staying in the dark room. Why shouldn’t an agent decrease the strength of its predictions that the world will change, that it will perform diverse acts in the future, or that it will inhabit high surprisal states? Insofar as any one of these strategies would lead to the avoidance of dark rooms, it is unclear why the internalist response should be preferred.7 At the same time, it is unclear why exactly this choice is to be preferred over the alternative of staying in the dark room. In other words, any of the proposed models, understood in such a way that the predictions are all malleable, might explain why an organism left the dark room (if it did); but they can equally well explain why an organism stayed in the dark room (if it does).8

There is an extended (or embodied) counterpart to the internalistic response that may be better suited to avoiding dark rooms. According to this extended view, some predictions or priors are kept stable by tying them to fixed features of the organism or its environment. For example, Karl Friston expresses it as follows:

[E]very organism (from viruses to vegans) can be regarded as a model of its econiche, which has been optimized to predict and sample from that econiche. [...] This means that a dark room will afford low levels of surprise if, and only if, the agent has been optimized by evolution (or neurodevelopment) to predict and inhabit it. Agents that predict rich stimulating environments will find the “dark room” surprising and will leave at the earliest opportunity. This would be a bit like arriving at the football match and finding the ground empty. (Friston et al. 2012, p. 3)

Crucially, on this response, “model” encompasses the system’s “interpretive disposition, morphology, and neural architecture, and as implying a highly tuned ‘fit’ between the active, embodied organism and the embedding environment” (Friston et al. 2012, p. 6). This answer is not fully internalistic, but mixes internal and external aspects. Specifically, it assumes a matching of external factors, such as the configuration of the ecological niche an embodied cognitive system inhabits, with the internal model the organism has of that niche. On this extended response, we do not dwell in dark rooms because we are embodied agents that need to sustain homeostasis in a world where means and resources are unevenly spread in a changing environment (Klein in press), and we represent the world as such.9

This extended response is better suited to answering the dark room problem than the internalist alternative, because some of the model’s predictions are in fact ineligible for Bayesian updating: an animal’s morphology or fit to its econiche cannot be altered in the same quick way as its internal representations. For this reason, the argument against the purely internalistic answer outlined above does not apply: if some of the predictions of change, motion, exploration, and search are embodied rather than represented, they necessarily remain fixed. Thus, there is only one way for such agents to act, as they cannot adjust these embodied priors.10 For embodied systems, moving into a dark room will not decrease the likelihood of predictions of change, exploration, motion, nor change or alter their influence on behavior. Rather, these predictions are anchored in the body and its adaptation to the specific econiche of the organism (see also Bruineberg et al. forthcoming). Therefore, going into a dark room is not an option for any systems not adapted to caves; anything but sessile cave dwellers will inherently prefer dynamic environments.

By adopting an extended or embodied solution to the dark room problem, HPC departs from the brain-centric focus advocated by some of its proponents (e.g. Hohwy 2013). Unfortunately, this has the disadvantage of blurring a cognitive system’s boundaries. By viewing a system’s morphology and econiche as being part-and-parcel of its “model” of the environment, we lose the clear demarcation between the evidence that is available to the system and what this is evidence for (see Hohwy 2016 as well as Hohwy 2017, and Clark 2017). Intuitively, there should be a difference between predictions made and the evidence that is used to evaluate them. Hohwy 2016 expresses this view when he argues that there should be a tightly woven evidentiary blanket which makes part of the world, as well as our own bodies, cognitively unavailable to us—their properties are to be inferred but are not directly available or immediately known. If morphology and ecological niche are themselves part of the model, however, this evidentiary blanket is lost. Therefore, this solution is unlikely to be attractive to those proponents of HPC who hope to retain a clear distinction between predictive mind and predicted world (see also Hohwy 2013).

Is there a way to retain the sharp boundary between internal and external while also getting the benefits of the extended response? Here, the tools and methods of BRA might complement the ones of HPC. BRA is purpose-built for specifying the task environments inhabited by particular cognitive systems. Indeed, BRA-theorists have developed specialized techniques with which to formalize assumptions, including about the nature of the hypothesis space being considered; the prior knowledge possessed; the likelihood of experiencing particular stimuli given that certain hypotheses are true for an environment; and perhaps most importantly, the relative costs or benefits of particular actions in a particular environment (Anderson 1991; Oaksford and Chater 2007). Recall that proponents of BRA invoke Bayes’ rule to compute posterior probability distributions over a space of, for example, possible causes of a particular visual stimulus. Thus, they assume that real-world behavior depends not only on an estimation of which causes are the most probable, but also on a calculation of which course of action is the most prudent. Indeed, behavioral actions typically have consequences that should influence whether or not they are actually performed: to any villainous inhabitant of Metropolis, erroneously classifying Superman as a bird (leading to a false feeling of security, detection, and swift justice) will be more costly than erroneously classifying a bird as Superman (which merely incurs ridicule). For this reason, even if the posterior probability of “It’s a bird!” is high, the villain’s best course of action might be to declare “It’s Superman!” in order to avoid swift justice. Notably, Bayesian Decision Theory may be used to specify how posterior probability distributions should be combined with cost functions that formalize such consequences, so as to minimize the expected costs to the organism. Proponents of the BRA modeling framework regularly incorporate such cost functions into their computational-level characterizations of human and animal behavior (for discussion see e.g. Gershman and Daw 2012).

Some HPC-theorists are averse to invoking formal constructs such as cost functions that go beyond the calculation of probably distributions—some actively avoid them or think that they can do without (see Schwartenbeck et al. 2013 and Friston et al. 2012). But there are reasons to think this aversion is ill-advised. First, cost functions are just the kind of formal construct that may be needed to add precision to Clark’s rather intuitive appeal to “change, motion, exploration, and search” and related proposals by other HPC-theorists. Whereas dark-room-seeking behavior could be associated with a high cost to the organism, explorative behavior might be rewarded. In this way, BRA provides formal interpretational tools that help to describe why going into a dark room is in fact unreasonable given a dynamic environment where resources are unevenly spread. HPC might have formal tools to model under which circumstances an organism does not go into the dark room. But what is lacking is a tool for evaluating the extent to which this behavior can be seen as reasonable or prudent. As well as adding further formal tools to the Bayesian toolkit, BRA and Bayesian Decision Theory together provide an interpretational tool for understanding behavior. These interpretational tools can be used to supplement the suspicions of HPC-theorists that dark-room-dwelling would be detrimental to an organism, by precisely modeling the system’s behavior in relation to its environment in a way that the customary tools and concepts of HPC cannot. At the same time, these tools do not require that a cognitive system’s body and econiche themselves be viewed as a “model”. Rather, bodily features and environmental constraints are encoded as costs and benefits that are poised to influence the relevant system’s behavior.

Thus supplemented by the tools of BRA and Bayesian Decision Theory, the HPC modeling framework has a way of explaining why cognizers generally avoid dark rooms, while retaining a clear distinction between cognizers and their environment. However, some HPC-theorists reject this story as they maintain that as long as we minimize surprisal in our world, exploration and high-utility-gaining states come naturally. For example, Schwartenbeck et al. 2013 write that:

[M]inimizing surprise leads naturally to concepts such as exploration and novelty bonuses. In this approach, agents infer a policy that minimizes surprise by minimizing the difference (or relative entropy) between likely and desired outcomes, which involves both pursuing the goal-state that has the highest expected utility (often termed “exploitation”) and visiting a number of different goal-states (“exploration”). (Schwartenbeck et al. 2013, p. 1)

Views like these bring us to another proposal of how BRA contributes to HPC, because they raise the question: why does such behavior lead to the highest expected utility? One can only say that it maximizes expected utility if a model of the environment is implicitly presumed where such behavior does maximize expected utility. The tools of BRA are ideally suited to make this implicit model of the organism-environment-coupling explicit.

We also believe that including the formal tools of BRA circumvents another problem of HPC-accounts: only HPC-accounts with fixed and stable (or at least specific) priors can account for observed behavior which is stable across organisms of a species. But how do such fixed priors come to be? HPC-theorists ought to give some explanation as to why we have the priors we have which explain the behavior we show. Giving such explanations often involves references to the environment in which an organism evolved and developed. But Hohwy (Hohwy 2013; see also Bowers and Davis 2012) warns us of Bayesian just-so stories, where we merely hypothesize about how a prior might arise without actually checking for evidence for such stories:

The challenge […] is to avoid just-so stories. That requires avoiding priors and likelihoods that are posited only in order to make them fit an observed phenomenon. To avoid just-so stories any particular ordering of priors and likelihoods should be supported by independent evidence, which would suggest that this ordering holds across domains. (Hohwy 2013, p. 94)

One source of such independent evidence for specific priors might come from BRA, where we model the environment with its specific features, distribution of resources, and the costs and benefits for certain actions. This then might serve as a tool for distinguishing Bayesian just-so stories or how-possibly-explanations from how-actually-explanations. Supplementing a successful HPC-story with some of BRA’s tools then gives us a broader Bayesian explanation of the behavior we exhibit and the mind that brings it about.11

Therefore, we believe that BRA complements HPC. First, because only HPC-solutions where some priors are fixed or ineligible for Bayesian updating can explain why all nontroglobionitic animals avoid dark rooms. A prominent solution for this is an extended account where certain stable features of both organism and environment are part of the organism’s model, thereby fixing certain priors. However, this endangers the strong evidentiary blanket, which some HPC-theorists like to maintain. In order to preserve this blanket, the tools of BRA can be used to explain why certain behaviors come with certain costs and benefits and are therefore performed. Second, because BRA provides an interpretational tool, telling us why certain behaviors are prudent. Third, if we avoid cost-functions and argue that minimizing surprisal comes with high expected utility, our best evidence for this is an implicit model of the environment, which can best be made explicit by using BRA. Fourth, if HPC-explanations rely on specific priors, BRA may help us to distinguish Bayesian how-possibly-explanations (just-so stories) from how-actually-explanations. We take these reasons as sufficient for advocating a combination of BRA and HPC.

5Conclusion

We have sought to clarify how the Bayesian Rational Analysis and Hierarchical Predictive Coding modeling frameworks relate, and did so by comparing them vis-à-vis Marr’s influential three-level conception of explanation in cognitive science. Whereas BRA-theorists answer questions at the computational level of analysis only, HPC-theorists focus primarily on the algorithmic level, while also addressing the computational and implementational levels. Given that answering questions at the computational level is insufficient for full-fledged explanation, the methods and practices of HPC can appear to offer a far more likely avenue to explanatory success. Nevertheless, because BRA (i) appears well-suited for supporting a solution to the dark room problem due to its specific tools and concepts for modeling task environments, (ii) provides an interpretational tool (iii) allows us to make implicit assumptions about the structure of the environment explicit, and (iv) helps to distinguish how-possibly- from how-actually-explanations, it appears that three-level explanations of behavior and cognition are most likely to be forthcoming if the Bayesian Rational Analysis and Hierarchical Predictive Coding frameworks are combined.

References

Anderson, J. R. (1991). Is human cognition adaptive? Behavioral and Brain Sciences, 14 (3), 471–485.

Bastos, A. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries, P. & Friston, K. J. (2012). Canonical microcircuits for predictive coding. Neuron, 76, 695–711.

Bechtel, W. & Richardson, R. C. (1993). Discovering complexity. Decomposition and localization as strategies in scientific research. Cambridge, MA: MIT Press.

Bowers, J. S. & Davis, C. J. (2012). Bayesian just-so stories in psychology and neuroscience. Psychological Bulletin, 138 (3), 389–414. https://dx.doi.org/10.1037/a0026450.

Bruineberg, J., Kiverstein, J. & Rietveld, E. (forthcoming). The anticipating brain is not a scientist: The free-energy principle from an ecological-enactive perspective. Synthese. https://dx.doi.org/10.1007/s11229-016-1239-1.

Clark, A. (2013). Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behavioral and Brain Sciences, 36 (3), 181–204.

——— (2017). How to knit your own Markov blanket: Resisting the second law with metamorphic minds. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Colombo, M. & Series, P. (2012). Bayes in the brain–On Bayesian modelling in neuroscience. British Journal for the Philosophy of Science, 63 (3), 697–723.

Danks, D. (2008). Rational analyses, instrumentalism, and implementations. In N. Chater & M. Oaksford (Eds.) The probabilistic mind: Prospects for Bayesian cognitive science (pp. 59–75). Oxford: Oxford University Press.

Ernst, M. O. & Banks, M. S. (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature, 415 (6870), 429–433. http://dx.doi.org/10.1038/415429a.

Friston, K. (2005). A theory of cortical responses. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 360 (1456), 815–836. https://dx.doi.org/10.1098/rstb.2005.1622.

——— (2009). The free-energy principle: A rough guide to the brain? Trends in Cognitive Sciences, 13 (7), 293–301.

——— (2010). The free-energy principle: A unified brain theory? Nature Reviews Neuroscience, 11 (2), 127–138. http://dx.doi.org/10.1038/nrn2787.

Friston, K., Thornton, C. & Clark, A. (2012). Free-energy minimization and the dark-room problem. Frontiers in Psychology, 3.

Gershman, S. J. & Daw, N. D. (2012). Perception, action and utility: The tangled skein. In M. I. Rabinovich, K. J. Friston & P. Varona (Eds.) Principles of brain dynamics: Global state interactions. MIT Press.

Griffiths, T. L. & Tenenbaum, J. B. (2006). Optimal predictions in everyday cognition. Psychological Science, 17 (9), 767-773. https://dx.doi.org/10.1111/j.1467-9280.2006.01780.x. http://pss.sagepub.com/content/ 17/9/767.abstract.

Griffiths, T. L., Kemp, C. & Tenenbaum, J. B. (2008). Bayesian models of cognition. In R. Sun (Ed.) The Cambridge handbook of computational cognitive modeling. Cambridge, UK: Cambridge University Press.

Griffiths, T. L., Chater, N., Norris, D. & Pouget, A. (2012). How the Bayesians got their beliefs (and what those beliefs actually are): Comment on bowers and davis (2012). Psychological Bulletin, 138 (3), 415–422. https://dx.doi.org/10.1037/a0026884.

Griffiths, T. L., Lieder, F. & Goodman, N. D. (2015). Rational use of cognitive resources: Levels of analysis between the computational and the algorithmic. Topics in Cognitive Science, 7 (2), 217–229.

Harkness, D. L. & Keshava, A. (2017). Moving from the what to the how and where – Bayesian models and predictive processing. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Hohwy, J. (2013). The predictive mind. Oxford University Press.

——— (2016). The self-evidencing brain. Nous, 50 (2), 259–285.

——— (2017). How to entrain your evil demon. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Jones, M. & Love, B. C. (2011). Bayesian fundamentalism or enlightenment? On the explanatory status and theoretical contributions of Bayesian models of cognition. Behavioral and Brain Sciences, 34 (4), 169–188.

Klein, C. (in press). What do predictive coders want? Synthese. https://dx.doi.org/10.1007/s11229-016-1250-6.

Knill, D.C & Pouget, A. (2004). The Bayesian brain: The role of uncertainty in neural coding and computation. Trends in Neurosciences, 27 (12), 712–719. https://dx.doi.org/10.1016/j.tins.2004.10.007.

Kwisthout, J. & van Rooij, I. (2013). Bridging the gap between theory and practice of approximate Bayesian inference. Cognitive Systems Research, (24), 2–8.

Körding, K. P. & Wolpert, D. M. (2004). Bayesian integration in sensorimotor learning. Nature, 427 (6971), 244–247. http://dx.doi.org/10.1038/nature02169.

Ma, W. J., Beck, J. M., Latham, P. E. & Pouget, A. (2006). Bayesian inference with probabilistic population codes. Nature Neuroscience, 9 (11), 1432–1438. http://dx.doi.org/10.1038/nn1790.

Maloney, L.T. & Mamassian, P. (2009). Bayesian decision theory as a model of human visual perception: Testing Bayesian transfer. Visual Neuroscience, 26, 147–155.

Marr, D. (1982). Vision: A computational approach. San Francisco: Freeman.

McClamrock, R. (1991). Marr‘s three levels: A re-evaluation. Minds and Machines, 1 (2), 185–196. https://dx.doi.org/10.1007/BF00361036.

Mumford, D. (1992). On the computational architecture of the neocortex. II. The role of cortico-cortical loops. Biological Cybernetics, 66 (3), 241–251.

Oaksford, M. (2001). The probabilistic approach to human reasoning. Trends in Cognitive Sciences, 5 (8), 349–357.

Oaksford, M. & Chater, N. (2007). Bayesian rationality: The probabilistic approach to human reasoning. Oxford: Oxford University Press.

Piccinini, G. & Craver, C. F. (2011). Integrating psychology and neuroscience: Functional analyses as mechanism sketches. Synthese, 183 (3), 283–311.

Rao, R. P. N. & Ballard, D. H. (1999). Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nature Neuroscience, 2 (1), 79–87. http://dx.doi.org/10.1038/4580.

Sanborn, A. N., Griffiths, T. L. & Navarro, D. J. (2010). Rational approximations to rational models: Alternative algorithms for category learning. Psychological Review, 117 (4), 1144–1167.

Schwartenbeck, P., FitzGerald, T., Dolan, R. J. & Friston, K. (2013). Exploration, novelty, surprise, and free energy minimization. Frontiers in Psychology, 4 (710), 1–5.

Shagrir, O. (2010). Marr on computational-level theories. Philosophy of Science, 77 (4), 477–500.

Sims, A. (2017). The problems with prediction. The dark room problem and the scope dispute. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.

Spratling, M. W. (2013). Distinguishing theory from implementation in predictive coding accounts of brain function. Behavioral and Brain Sciences, 36 (3), 231–232.

Von Helmholtz, H. (1867). Handbuch der physiologischen Optik. Leipzig: Leopold Voss.

Xu, F. & Tenenbaum, J. B. (2007). Word learning as Bayesian inference. Psychological Review, 114 (2), 245–272.

Zednik, C. (2017). Mechanisms in cognitive science. In S. Glennan & P. Illari (Eds.) The Routledge handbook of mechanisms and mechanical philosophy. London: Routledge.

Zednik, C. & Jäkel, F. (2016). Bayesian reverse-engineering considered as a research strategy for cognitive science. Synthese 193: 3951. https://dx.doi.org/10.1007/s11229-016-1180-3.