Literal Perceptual Inference
In this paper, I argue that theories of perception that appeal to Helmholtz’s idea of unconscious inference (“Helmholtzian” theories) should be taken literally, i.e. that the inferences appealed to in such theories are inferences in the full sense of the term, as employed elsewhere in philosophy and in ordinary discourse. The argument consists in first defending a minimal conception of inference based on Gilbert Harman’s account (Harman 1973), and then arguing that Helmholtzian computational models of perceptual inference such as those proposed in Hinton and Sejnowski 1983, Hinton et al. 1995, and Friston 2005 implement the type of process Harman describes.
In the course of the argument, I consider constraints on inference based on the idea that inference is a deliberate action (Boghossian 2014; Broome 2014; Wright 2014), and on the idea that inferences depend on the syntactic structure of representations (Mandelbaum 2016). I argue that inference is a personal-level but sometimes unconscious process that cannot in general be distinguished from association on the basis of the structures of the representations over which it’s defined. I also critique the argument against representationalist interpretations of Helmholtzian theories in Orlandi 2015, and argue against the view that perceptual inference is encapsulated in a module.
Keywords
Artificial neural networks | Bayesian Inference | Free energy minimization | Generative models | Induction | Inference | Perceptual inference | Predictive processing | Representation
Acknowledgements
I would like to thank the anonymous reviewers of this paper, as well as Grace Helton, Geoffrey Hinton, Jakob Hohwy, Zoe Jenkin, Hakwan Lau, Eric Mandelbaum, Thomas Metzinger, Nico Orlandi, Jona Vance, David Papineau, Jake Quilty-Dunn, David Rosenthal, Wanja Wiese, and the Cognitive Science group at the CUNY Graduate Center, for conversations and suggestions that have informed my thinking on these matters.
1Introduction
Helmholtz proposed the idea, so influential within recent cognitive science, that what we perceive in sensory experience is the conclusion of unconscious inductive inference from sensory stimulation. Less famously, he questioned whether the term ‘conclusion’ could be applied to the deliverances of perception in the same “ordinary” sense in which it is applied to conscious acts of reasoning (Von Helmholtz 1860/1962, p. 4). This is not, of course, a merely verbal question. If we know that a term such as ‘knowledge’, ‘memory’, or ‘inference’ is being used in an unusual sense, we should be able to articulate the difference between this sense and the usual one, and to that extent we must understand the nature of the corresponding phenomenon.
Helmholtzian theories of perception thus put philosophical pressure on the concept of inference. Such theories include predictive processing models (Friston 2005; Rao and Sejnowski 2002; Huang and Rao 2011; see Clark 2013 and Hohwy 2013 for discussion), as well as many models of perception in machine learning that in part inspired the predictive processing framework, notably those discussed in Hinton and Sejnowski 1983, Hinton et al. 1995, and Hinton 2007, as well as Oh and Seung 1997 and many others.1 Taken at face value, these theories are committed to the view that the representations underlying perceptual experiences are literally the conclusions of inductive inferences, taking sensory representations and background knowledge or memories as premises (Aggelopoulos 2015). In this paper, I argue that the literal interpretation of such theories is warranted, and that apart from the lack of conscious awareness that gave Helmholtz pause, which may be regarded as inessential to inferential mechanisms themselves, there is no compelling reason to deny that Helmholtzian perceptual inference is the genuine article.
In this section, I attempt to provide a well-motivated account of inference as a psychological process, independently of any role it may play in perception. The account draws heavily on Gilbert Harman’s work (Harman 1973), which gives a central role to the notion of coherence. In the second section of the paper, I first argue that this account of inference, though couched in terms of propositional attitudes, can plausibly subsume processes defined over sensory representations. I then describe in detail how I take perceptual inference to be realized in Helmholtzian computational models.
2.1Inference as Reasoned Change in View
A general account of inference must cover all paradigmatic uses of the term ‘inference’—most saliently, it should accommodate deductive reasoning as well as various sorts of ampliative reasoning, such as enumerative induction and abduction or “inference to the best explanation”. Paul Boghossian, following Harman (Harman 1986), offers an intuitively plausible characterization of inference as a “reasoned change in view”: a process “in which you start off with some beliefs and then, after a process of reasoning, end up either adding some new beliefs, or giving up some old beliefs, or both” (Boghossian 2014, p. 2). This first pass must be generalized in certain ways.
First, we should make room for processes of reasoning that alter degrees of belief or subjective probabilities without necessarily resulting in the wholesale dropping or adding of beliefs. Such processes intuitively fit the description ‘reasoned change in view’, and Boghossian could be viewed as describing a special case in which probabilities are changed to or from zero. Second, in hypothetical reasoning, certainly a paradigm of inference, one may infer Q from P without believing either, for example to explore the consequences of a counterfactual. Thus, the above description should be modified so that it appeals to some weaker attitude than belief, such as provisional acceptance (Wright 2014, p. 29).2 I alternate between the two formulations in what follows, noting where a generalization to acceptance raises special issues.
Clearly, inference so conceived may involve more than just drawing new conclusions from premises. It may, for example, involve lowering the probability of previously held beliefs based on new evidence, or rejecting the premise of an argument whose conclusion is inconsistent with an entrenched belief. It is thus not clear that inference in general can be modeled on simple syllogistic reasoning.
Consider for example a change in belief that takes P and P → Q as premises and, instead of resulting in the belief that Q, results in the rejection of P → Q (Harman 1973, p. 157). This could perhaps be understood as a chain of inferences in which one first infers Q from the premises, and then infers from the combination of Q and one’s prior belief that ~Q that one must have been mistaken about P→Q (a reductio). There are at least two concerns about this proposal, however: one must momentarily believe both Q and ~Q (or assign probabilities to these propositions that sum to more than 1), and some grounds must be supplied for rejecting P → Q rather than P.
These examples suggest that inference involves more than consideration of relations of logical implication even where such relations are relevant. Harman (Harman 1973, ch. 10, section 4) takes this to show that there are no distinctively deductive inferences, as opposed to deductive arguments. Boghossian (Boghossian 2014, p. 5), similarly, suggests that deduction can be distinguished from induction in terms of the standards for evaluation (logical entailment VS probabilistic support) that (one takes to) apply to one’s inference, but that this distinction gives us no reason to suppose that there are two intrinsically different types of inference. I’ll provisionally assume that Harman and Boghossian are right about this, and return to the point shortly.
Harman (Harman 1973) develops an account of inference designed to handle examples like the above. He conceives of inference not as a serial process akin to mentally traversing a syllogism, but as a parallel process that takes one’s total current evidence as input and yields a new total set of beliefs (Harman 1973, p. 159):
A more accurate conception of inductive inference takes it to be a way of modifying what we believe by addition and subtraction of beliefs. Our “premises” are all our antecedent beliefs; our “conclusion” is our total resulting view. Our conclusion is not a simple explanatory statement but a more or less complete explanatory account.
On Harman’s account, all inference is essentially inference to the best explanation (where some “explanations”, as in deductive inferences, are arguably trivial). In the following paragraph Harman suggests that this inferential process is constrained by two competing principles, coherence-maximization and change-minimization:
Induction is an attempt to increase the explanatory coherence of our view, making it more complete, less ad hoc, more plausible. At the same time we are conservative. We seek to minimize change. We attempt to make the least change in our antecedent view that will maximize explanatory coherence.
Harman’s characterization of coherence is rather laconic, but Laurence BonJour (BonJour 1985) articulates a serviceable notion that is consistent with Harman’s usage, and which I will assume in what follows. According to BonJour, a coherent set of beliefs must minimally be largely logically consistent, as well as enjoying a high degree of consistency between the probabilities and truth-values assigned to its members (e.g. the combination “p” and “It is highly improbable that p” lessens coherence). Lack of inconsistency is not sufficient for coherence, however, since a set of unrelated beliefs may be internally consistent without intuitively cohering. Thus, BonJour supposes in addition that coherence is increased with “the number and strength of inferential connections” between members of a consistent collection of beliefs (BonJour 1985, p. 98). On this assumption, beliefs in (non-trivial) explanatory statements (e.g. scientific laws) greatly enhance the coherence of a system, since they are typically inferentially related to many other beliefs.
Harman’s coherence-based account allows hypothesis testing to be viewed as a special case of inference in which one of the premises is an observation that may not cohere with existing belief. Thus, the Duhem-Quine thesis about confirmation holism (Quine 1951) applies also to inference as Harman characterizes it. This holism can explain why the premises that lead to an unacceptable conclusion may be treated differently during belief-revision: they may stand in different evidential relations to the other things one believes.
This account of inference also provides a compelling way to avoid the lottery paradox3 and similar cases. We do not know that any particular ticket in the lottery will lose because our evidence doesn’t favor any one ticket winning over the others. All the alternatives are equally coherent, so no total view containing the belief that a particular ticket will lose can be inferred (Harman 1973, p. 160; see also Lehrer 1986, pp. 155-156).4
Generalizing Harman’s account to acceptances may seem problematic, because what distinguishes acceptances from beliefs is precisely that they do not depend on, and indeed must be capable of conflicting with, one’s beliefs. For this reason, I do not take it to be a constraint on all inference that it be holistic in the sense that any inference must take as input one’s total body of evidence (though some inferences may do so). Harman’s account can be extended to acceptances and thus to hypothetical reasoning by supposing that the same type of holistic process that governs rational change in belief governs rational change in acceptance, where the range of acceptances taken as input to the process depends on the context and is distinct from one’s set of beliefs. Given this extension, syllogistic reasoning such as that involved in deduction can be construed as reasoning in which only a very small set of acceptances is considered.
Thus far inference has been characterized as a process that modifies (degrees of) belief (or acceptance, more broadly), such that coherence among beliefs (or acceptances) is maximized. Implicit in this account is the idea that changing one’s view in a way that results in greater coherence is rational. In this section I discuss how standards of rationality for inductive and deductive reasoning may be taken on board by this type of account.
Logical implication is of course a paradigm of rational transition between representations. The rationality of a process in this sense is a matter of its tendency to preserve truth (necessarily, in the case of deductively valid inference). The rationality of induction may arguably be characterized in essentially the same way, as on BonJour’s (BonJour 1985, p. 96) view that inference must be “to some degree” truth-preserving. Hume ’s skepticism about induction aside, inductive inference is a process that tends to yield true belief in worlds like ours.
The preceding assumes that modification of degrees of belief or subjective probability can be truth-preserving. There is precedent for this view in formal treatments of induction such as those offered by Reichenbach (Reichenbach 1949). Carnap (Carnap 1950), similarly, generalizes deductive consequence relations to “partial implications” (degrees of inductive support). A detailed treatment of this topic is beyond the scope of this paper, but correspondences between logical truth-functions and analogous rules for probability suggest that at least simple truth-functions of propositional logic can be viewed as special cases of the axioms of probability theory in which the relevant probabilities are Boolean truth values, assuming independence for the probabilities:
|
Expression |
Boolean truth function |
Probability |
|
A ^ B |
A * B |
p(A) * p(B) |
|
A v B |
A + B – (A * B) |
p(A) + p(B) – p(A)p(B) |
|
~ A |
1 – A |
1 – p(A) |
Figure 1. Simple truth functions in propositional logic as special cases of rules relating probabilities.
More systematically, an obvious way of understanding probability in terms of truth is to adopt a generalized frequentist account according to which probabilities are measures of frequency relative to sets of situations, actual or hypothetical. From this perspective conditional probabilities, Bayesian subjective probabilities, and modal claims (including implicitly modal claims such as subjunctive conditionals) can be treated similarly. Subjective probabilities may be regarded as frequencies relative to a set of possible worlds consistent with one’s evidence.
Instantiation of a psychological process can thus be considered an exercise of (theoretical) rationality5 to the extent that we have reason to believe it will yield true outputs given true inputs (both actually and counterfactually), where truth may be evaluated in a single situation only or simultaneously in a range of situations. Inferences that result in dropping beliefs may fit this description, since dropping a belief may be a way of avoiding believing something false. And when large collections of representations are involved, truth-preserving transition amounts to maximization of coherence.
The most pressing objection to the account sketched so far is that, since it picks out inferential processes as just those processes that conform to a standard of rationality, no inference can fail to conform to this standard. As Boghossian (Boghossian 2014, p. 4) puts it in discussing a similar proposal, “if one is reasoning at all, one is reasoning to a conclusion that one has justification to draw”. Of course, a process may tend toward truth-preservation but fail to preserve truth in a particular case. But simple appeal to a type-token distinction cannot meet the objection, because there seem to be types of reasoning that fail to yield true beliefs—systematic failures of rationality such as base rate neglect and denial of the antecedent (Wright 2014, p. 37).
An advocate of the present account of inference needn’t deny, however, that the latter are species of reasoning. One possible response is to appeal to a hierarchy of types, rather than a simple type-token distinction. Systematic errors in reasoning may be due to the application of heuristics that are effective in one domain to analogous domains in which they fail. Consistent with this suggestion, Gerd Gigerenzer claims that agents often approach cognitive problems not by performing optimal inference in conformity with strict canons of rationality, but instead by in effect substituting for the target problem a simpler one that is easier to solve and, at least in the given context, may be just as likely or more likely to succeed than the ideally rational method (Gigerenzer calls this the “ecological rationality” of heuristics—see, e.g. Goldstein and Gigerenzer 2002).6 Though Gigerenzer appeals to this mechanism to explain successful inference, it may also explain cases of cognitive failure in a way that preserves their rationality, as suggested here.
A more substantial response, one which I favor but which needs elaboration and defense beyond what can be given here, is that apparent systematic failures of rationality are systematic failures to represent the target problem correctly. Base rate neglect, for example, is a failure to take base rates into account in inferring probabilities, but corresponds to optimal Bayesian inference given that the base rate is neglected, i.e. if the actual base rate is replaced with 0.5 in Bayes’s theorem. In the case of denial of the antecedent, we may suppose that reasoners ignore the deductive validity of the argument and simply consider whether Q is likely to be the case, given only the information that P → Q and ~P. Absent any other reason to believe Q, denial of the antecedent is rational and amounts to assuming Q only if P, i.e. Q → P. This is a misrepresentation of the original argument in question, but is correct reasoning given that misrepresentation. To take one more example: the reasoning that goes on when one affirms the consequent may be regarded, simply, as an inference to the best explanation of Q, where P is the only contextually available explanation.
John Anderson suggests just such a treatment of apparent irrationality, which is worth quoting at length:
Many characterizations of human cognition as irrational make the error of treating the environment as being much more certain than it is. The worst and most common of these errors is to assume that the subject has a basis for knowing the information-processing demands of an experiment in as precise a way as the experimenter does. What is optimal in the micro-world created in the laboratory can be far from optimal in the world at large (Anderson 1991, p. 473).
Similar remarks apply to cases such as the latter two discussed above, in which a piece of reasoning “in the wild” that is sensible given partial information is evaluated against canons of deductive rationality that the subject may not be imposing. 7
2.3Reasoning as Deliberate Action
The foregoing conception of inference as rational change in view is rather minimal compared with recent accounts that emphasize the deliberate, conscious, personal-level character of paradigmatic reasoning. In this section, I consider such alternative views of what inference consists in, and argue that they either boil down to the minimal account or impose unwarranted constraints on inferential processes.
Boghossian argues that “Inferring necessarily involves the thinker taking his premises to support his conclusion and drawing his conclusion because of that fact” (Boghossian 2014, p. 5). ‘Taking’ here may be interpreted in a variety of ways: as having a further belief to the effect that the premises support the conclusion, as following an implicit or explicit rule of inference (Boghossian’s preferred interpretation), or as being disposed to give the premise(s) as reason(s) for the conclusion. The motivation for this “taking” condition is twofold: it distinguishes inferential processes from other causal transitions between representations, and it ensures that inference is something that one does with a goal, rather than something that simply happens, perhaps within a cognitive subsystem (see 3.2 below for further discussion of the latter possibility).
The minimal account defended above may satisfy the “taking” condition on a weak enough reading. Taking a conclusion to follow from some premises may simply be a matter of regularly inferring the conclusion from the premises, or being disposed to do so, ceteris paribus, where inferring is already distinguished from mere causal connection (and from irrational or arational association, should there be such a thing) by the rationality, in the sense of subjunctively truth-preserving character, of the transition.
One concern here is that, while Harman’s account of reasoning rules out the possibility of its occurring within a module due to its holism, the modification of the account to include reasoning over acceptances seems to sacrifice this feature. But it’s plausible that reasoning over acceptances relies on the same implicit background beliefs as ordinary reasoning, and so still requires access to general world knowledge. The inferential models of perception discussed in the next section of the paper are consistent with this possibility.
Still, the minimal account would likely not do justice to “taking” as Boghossian intends it, because such inference may for all that’s been said occur automatically and unconsciously, and Boghossian is explicitly concerned to give an account of deliberate, conscious, “System 2” reasoning. But it’s not clear that all inference is done deliberately (consider drawing a conclusion one doesn’t like in spite of oneself). And it begs the question against the minimal account to suppose that reasoning that occurs consciously differs, qua reasoning, from reasoning that occurs without consciousness. This is so even if one grants that inference is by definition a personal-level, goal-directed activity, since one may do things purposefully but without awareness of doing them. One may, for example, take a break from working on a cognitively demanding problem and wake from a nap with the solution. The obvious explanation of cases like this is that one has been reasoning unconsciously.8
John Broome (Broome 2014) agrees with Boghossian that reasoning is a matter of rule-following, and offers an account of following a rule in terms of a complex disposition: to follow a rule in doing X is to have a disposition both to do X and for doing X to seem “right” to you with respect to the relevant rule. The second clause distinguishes reasoning from mere causation (Broome 2014, p. 21). Broome suggests that this account satisfies Boghossian’s “taking” condition in something like the weak way suggested earlier.
But it is not clear why the simple disposition to conclude Q from P isn’t sufficient for inference, where the connection between P and Q is rational. Animals that employ fewer higher-order monitoring mechanisms than humans do can plausibly still reason, at least in limited ways. Such animals may have no disposition for their inferences to seem correct to them. While Broome doesn’t require that inference involve conscious “taking”, his account still requires meta-representation that needn’t be supposed essential to inference, especially if a more minimal account is viable.
Crispin Wright rejects Boghossian’s “taking condition” and supposes simply that inference is a matter of accepting a conclusion for the reason that one accepts the premises (Wright 2014, p. 33), which is a case of acting for reasons more generally. Wright is clear that on his view acting for reasons is not a matter of meta-representation but rather a matter of acting in a way that conforms to constitutive constraints on rational action (p. 35). In particular, he claims that acting “in accordance with basic rules of inference is constitutive of rational thought” (p. 36).
Since preserving truth is arguably the constitutive norm on rational thought, the minimal account plausibly satisfies Wright’s description. If one arrives at a set of acceptances C as a result of a rational process that takes another set R as input, one may be said to accept C for the reason that one accepted R. It is less obvious whether the minimal account can be extended to action generally, unless action can be said to preserve truth in the way that inference can.9 Wright does not, in any case, offer an analysis of acting for reasons, so the minimal proposal has no clear competitor with respect to this issue.
2.4Inference, Association and Compositional Structure
I have so far said nothing about what, if anything, distinguishes inference from association. This issue may seem particularly pressing given the connectionist (and therefore, some would argue, associationist) pedigree of Helmholtzian computational models of perception. Though his primary concern is not to give an account of inference, Eric Mandelbaum (Mandelbaum 2016, p. 8, fn. 14) claims that inference is distinguishable from other sorts of mental transition between propositional contents in terms of its computational profile. In particular, in inference, “The mental transition between the premises and the conclusion occurs not because they were (e.g.) associated through prior learning, but instead because they conform to the logic of thought”, where the latter is a system of rules that governs transitions between mental representations, analogous to but likely distinct from classical logic.
What distinguishes this view from the rule-following proposals just discussed is the claim that the rules of the envisaged logic are sensitive to the formal or syntactic structure of the representations they govern: “A mental inference is a transition in thought that occurs because the argument structure instantiated the germane cognitive rules of inference.” Mandelbaum supposes that such rules operate on “Structured Beliefs”: representations whose relevant core features are that they (a) have compositional structure, (b) relatedly, have a proprietary syntax and semantics, and (c) sometimes enter into causal relations that mirror the “implicational structure” of their contents.
Clause (c) is clearly compatible with the view defended above, according to which syntactically specified rules in effect play no essential role in inference. Transitions likely to preserve truth can be picked out by appeal to a formal logic, but in order for a mental transition to be rational and thus inferential it is (on the minimal view) sufficient for it to in fact conform to the pattern of inferences defined by the logic.
What (a) and (b) add is, in effect, a psychologically realist interpretation of the logic, the internal structure of whose formulas is attributed to the corresponding mental representations by an inference to the best explanation. Presumably, this form of explanation amounts to the assumption that the relevant representational vehicles (neurons and populations of them in this case) contain reasonably concretely specifiable parts, possession of which explains why the causal interactions among the vehicles mirror the relevant structure of implications (see, e.g., Fodor 1975).
But appeal to such compositional structure cannot be used to define inferential transitions in general unless it is also taken to cover inductive inference. And it seems highly unlikely that any syntactic rules governing inductive inferences will serve to distinguish them from associations. This is not to say that structure has no role to play in understanding induction. It may be theoretically useful, for example, to bring simple enumerative inductions under the sway of syntax by treating their premises as conjunctions of the relevant evidential claims. But this requires only propositional logical structure as mediated by connectives, not subject-predicate structure internal to atomic sentences. This suggests that while the internal structure of representations may be the best explanation of certain types of inference, it is not a requirement on inferentially related representations generally.
Moreover, assume that the conditional probability of Q given P is the proportion of situations in which P obtains that are also situations in which Q obtains, and also that degree of inductive support in such simple cases as “It’s raining, therefore the streets are wet” can be defined in terms of conditional probability. In paradigm cases of associative learning, the strength of the association from P to Q depends in the same way on conditional probability, where the relevant set of situations is a sample consisting of observed cases. Thus, simple cases of induction may be indistinguishable from association between propositions, as Hume in effect contended.
Mandelbaum notes the difficulty of distinguishing inductive inferences from associations, but claims that associations are inherently symmetric (i.e. if P is associated with Q then Q is associated with P), which would serve to distinguish them (p. 6-7).10 Presumably, the symmetry of association is supposed to arise from the fact that strength of association depends on previous co-activation of representations, and co-activation is a symmetric relation.
Hebbian models of neural plasticity, however, suggest that association should be intrinsically asymmetrical, since the efficiency of a synapse from neuron a to neuron b depends on the extent to which firing of b is contingent on a’s having fired very recently, and not on the reverse relation. Symmetrical associations may as a matter of empirical fact be likely to occur as a result of associative learning, but on a Hebbian story this symmetry would be implemented via a pair of reciprocal synaptic connections, each of which would mediate a distinct associative link.11 This does not suggest a mechanism for association distinct from that subserving inductive inference. It may suggest also that though there is a clear distinction between paradigmatic rational belief revision and modification of associative structures by counter-conditioning or extinction, the representational changes caused by conditioning and by inductive inference are rational in the same sense.
While the foregoing discussion has been necessarily brief, I take it that the above considerations are sufficient to defend the minimal account of inference against pressing objections. In the next section I discuss perceptual inference and how it is modeled in several computational theories.
The recent wave of computational models based on Helmholtz’s theory propose that perception is a matter of inferring the best explanation of sensory input by inverting a generative model. A generative model (for present purposes) is a causal model that structurally mimics the process by which sensory input is generated (or more generally, any model capable of generating states of the input channel similar to those caused by the external world). Its inverse is a recognition model that maps from sensory input to explanations or, more narrowly, causes. This section of the paper explores how this idea is implemented in three distinct models, after consideration in the first two subsections of some putative reasons to doubt that perception could be based on inference.
It is uncontroversial that perception allows us to arrive at largely accurate judgments about what is in the environment on the basis of sensory input. This ensures that perceptual judgments are rationally related to knowledge of the inputs to the perceptual process. Therefore, what seems most relevant to evaluating Helmholtz’s theory is the claim that the inputs and outputs of the perceptual process are themselves truth-evaluable representations. There are challenges to this claim on both ends.
On the input side, it’s been argued that the proximal inputs to perceptual processes themselves should not be confused with the knowledge of those inputs that could serve as a basis for inference. Davidson (Davidson 1986), for example, criticizes Quine for conflating the causal intermediaries that lead from distal stimulus to belief with epistemic intermediaries in this way. And Tyler Burge agrees that “sensation does not play the role of data or evidence. Thinking that it does is the primary mistake of the sense-data tradition.” (Burge 2010, p. 367).
With respect to output, it’s not always clear how representations that are constitutive of perception itself can be distinguished from post-perceptual judgments (see Siegel 2010 for an attempt at providing a method for doing so, but also Quilty-Dunn unpublished for a critique), and it may be doubted whether perceptual experience always involves such judgments. The general project of distinguishing perception from cognition is of course arguably challenged by Helmholtzian theories, and it is difficult to address this issue without begging the question either way. Fortunately, any account of the inputs to perception according to which they are truth-evaluable will likely suffice to show that the same is true for representations further downstream, so that perception will turn out to involve inference no matter where one draws its upper boundary. And if the inputs to perception are not truth-evaluable, this suffices to show that perception is not inferential in the relevant sense.12
A possible reason to deny that perceptual representations could figure in inferences is that perceptual experiences seem to involve rich, non-discursive (e.g. iconic (Fodor 2007), qualitative (Rosenthal 2005), analog (Dretske 1981), or nonconceptual (Evans 1982)) contents. But it is not clear why a representation should fail to qualify as truth-evaluable simply because it occurs in an iconic, qualitative or otherwise special format. Arguably, all contents can be expressed in terms of an exhaustive enough (set of) proposition(s), so that format distinctions are orthogonal to the issue of whether a given content is truth-evaluable. This claim is liable to ring false if one assumes that genuinely truth-evaluable representations ipso facto possess language-like subject-predicate syntactic structure, but as we’ve seen, nothing about inference as such requires this.13
Perceptual contents are in any case clearly specifiable in terms of propositions, as Susanna Siegel (Siegel 2010) notes. Typically, each such proposition partially characterizes what is perceived in terms of one of its aspects—in other words, specifies a part of the overall perceptual content (for example, one may see, among other things, that the cat is green). If contents are the accuracy or veridicality conditions of representations (see, e.g., Burge 2010), it seems natural to identify perceptual contents with the sum of these parts, i.e. with the set of contents (truth-conditions) of the individual propositions sufficient to specify them. In Dretske’s somewhat idiosyncratic terms, sensory representations may carry many distinct pieces of information in an “analog” format.
More concretely, an iconic representation, for example, may be composed of an array of truth-evaluable representations that mark the light intensities across a visual field, or the relative positions of edges, or more generally, the components of any feature map.14 It is consistent with the models of perceptual processing discussed below to suppose that this decomposability of iconic perceptual content into propositional contents is reflected in vehicular structure, where each component representation is implemented by a neuron or neural population, corresponding to a node in a connectionist model (see e.g. Hinton and Sejnowski 1983). However, the basic claim about truth-evaluability is independent of this idea.
3.2Modularity and Sensory Representations
Perception is often supposed to be modular in nature, operating without influence from beliefs and responsive only to limited sources of information. If it is, then the causal intermediaries between sensory stimulation and perceptual judgment may at best be “subpersonal” or “subdoxastic” representations15, or perhaps not representational states at all (Orlandi 2015), in which case the theory of inference defended above would not apply to them (as mentioned already in 2.3).16
I cannot comprehensively address the modularity question here (see Zoe Drayson’s contribution to the present collection—Drayson 2017), but as mentioned previously, Helmholtzian theories arguably posit architectures that are nonmodular with respect to coarse-grained functional distinctions such as that between perception and cognition. Such theories are supported by mounting empirical pressure against modularity, which has given rise to debates over the “cognitive penetrability” of perception (Jenkin and Siegel 2015; Lupyan 2015), some specifically in the context of predictive coding theories (Newen et al. 2017).
For example, the existence of “extra-classical receptive field effects”, cited by Friston as evidence for his model (Friston 2005), constitutes a form of context-sensitive and therefore presumably rational top-down modification of early sensory representations (i.e. in striate cortex—see, e.g., Harrison et al. 2007). Top-down modification in some cases stems from sources in higher cognitive areas (for example, orbitofrontal cortex has been shown to modulate activity in temporal regions during object recognition—see O’Callaghan et al. 2017).
Drayson suggests that there are senses in which “predictive architectures” may nonetheless implement forms of modularity. In particular, though probabilistic dependence is transitive, she suggests, causal dependence needn’t be, so hierarchical models that implement Bayesian inference in their causal structures may exhibit a form of information encapsulation of one level relative to others (Drayson 2017, p. 9).17 But this sort of limited causal dependence, even if it sufficed for modularity, would not suggest that perceptual inference is encapsulated within a module. Perceptual inference, by hypothesis and as implemented in the computational models discussed below, is simply the process by which incoming sensory data is assimilated into a prior model of the world. This process may comprise many modular operations, but is itself as widely distributed throughout the hierarchy as is needed to facilitate the minimization of prediction error subsequent to the impact of sensory signals. It is therefore potentially holistic in the sense relevant to Harman’s account of inference.
Even if the mind is not modular, the representations involved in allegedly modular processes are widely supposed to differ importantly from beliefs. Stephen Stich (Stich 1978), for example, claims that “subdoxastic” representations differ from beliefs in that (a) they play very limited roles in inference, in contrast to beliefs which are “inferentially promiscuous”, (b) they are normally not accessible to conscious awareness, and (c) their contents may not correspond to anything the subject can comfortably be said to believe.
Feature (a) in Stich’s characterization poses no problem for present purposes, since it assumes that the states in question can play roles in inference. In any case, some beliefs are arguably much more restricted in their inferential roles than others, and it is to be expected on the basis of their contents alone that early sensory representations, which invariably concern concrete, context-bound particulars represented egocentrically, would exhibit comparatively limited inferential roles.
Feature (b) raises complex issues, but in brief, it is not clear that all representations involved in early and intermediate stages of perceptual processing normally occur without awareness. We are often visually aware of complexes of shapes, oriented edges, and other currently instantiated features of the environment represented in “low-level” vision, though not of the many constraints that seem to guide visual interpretation, such as the defeasible maxim “light comes from above”. 18 For present purposes, it does not matter whether the latter are considered dispositional beliefs or subdoxastic states in Stich’s sense, so long as transitions among the consciously accessible representations are inferential.
Stich’s final point (c) concerns the contents of allegedly subdoxastic states. The point may be put this way: suppose someone verbally expresses the belief “There is an edge oriented 20 degrees from vertical in the upper-left quadrant of my visual field.” Surely this person’s cognitive state differs from that of one who lacks the precise concepts QUADRANT and VERTICAL, even if this characterization captures the information carried by relevant sensory states. And if the verbally expressible state is what we normally attribute when we attribute belief, the sensory representation must be something else. This argument is compelling, but may suggest merely that the verbally sophisticated subject harbors more complex beliefs than, for example, a dog. Characterizing the content of the sensory state itself still poses a challenge, but this difficulty arises with respect to the cognitive states of nonhuman animals in any case.
More radically, Nico Orlandi (Orlandi 2015) argues that the causal antecedents of percepts are “representations” only in a trivial, too-liberal sense, and are better seen as detectors, indicators or biases, responsive only to their proximal causes. She claims that such states “do not model distal or absent conditions” (p. 19), and that they are not “map-like, pictorial or linguistic representations” (p. 25). They may cause the system to behave according to norms of rationality, but on Orlandi’s and similar views, transitions between such states, or from them to propositional attitudes, do not involve representations as premises, and so cannot be truth-preserving transitions.
However, many proponents of the theories under discussion understand representation in terms of the notion of structural homomorphism between model and environment (Hohwy 2013, ch. 8, Gładziejewski 2015), which Orlandi does not consider. On this view, the hierarchical model as a whole functions in a map-like way, even if its parts do not. Representations in the system get their contents in virtue of occupying positions in the system’s overall structure analogous to the positions occupied by represented facts or situations in the represented system. The intermediate states in perceptual processing hierarchies structurally represent causes at varying time-scales and thus model distal conditions. They may also model absent conditions, when the hierarchy is employed for non-perceptual purposes such as mental imagery or dreaming, or when illusion or hallucination occur. Moreover, such a system may need to be quite complex in order to have structure that can meaningfully correspond to environmental structure, so the relevant notion of representation is not trivial. A full defense of structural representation is firmly beyond the scope of this paper, but it suffices for present purposes to point out that the representationalist options considered by Orlandi are not exhaustive.
My aim in the preceding two sections has been to sketch a route around prima facie conceptual obstacles for the view that perception is the result of inference. The arguments offered have been necessarily both wide-ranging and brief, but I hope that those who disagree may nonetheless grant that the case for perceptual inference hinges on the outcome of these ancillary debates.
I turn now to computational models in the Helmholtzian tradition. Hinton & Sejnowski (Hinton and Sejnowski 1983) pioneered a model of “optimal perceptual inference” inspired in part by John Hopfield’s earlier work (Hopfield 1982). Though different from predictive processing models in important ways, it implements the idea that Bayesian inference can be accomplished via the minimization of potential energy within a generative model in a particularly transparent way. I first briefly describe the dynamics of the network, simply as a physical model of the brain, and then discuss the interpretation of the model as performing statistical inference.
The model consists of a large collection of binary stochastic processing units (“neurons”)—that is, units that may be in one of two states, 0 and 1, and whose states at any moment are determined probabilistically, using an activation function that computes the probability of a neuron being in the “1” state as a function of its weighted, summed input (plus a threshold or bias term). Each pair of units is reciprocally connected via symmetric synaptic weights, and a subset of the units additionally can receive input directly from an external information source. The network is otherwise unstructured.
Action potentials in a biological neuron are likely to occur in proportion to the voltage difference that has built up across its cell membrane (the “membrane potential”). This suggests that, as Hopfield (Hopfield 1982, p. 2555) puts it, “the mean rate at which action potentials are generated is a smooth function of the mean membrane potential.” This function turns out to be nonlinear, and in particular sigmoidal in shape (Figure 2a). Hinton & Sejnowski’s activation function (Figure 2b) models this function from potential energy to firing rate stochastically.
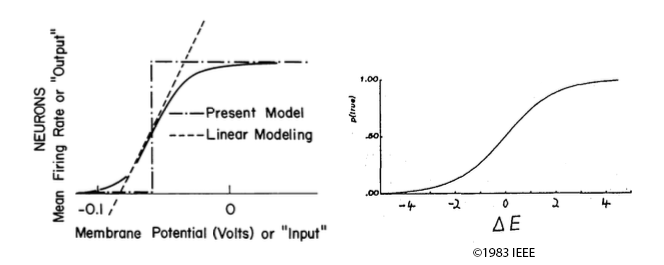
Figure 2. (a) The relationship between firing rates and membrane potential (Hopfield 1982, Fig. 1, reprinted with permission of the author). (b) The logistic activation function that maps an artificial neuron’s contribution to potential energy to its stochastic state (Hinton and Sejnowski 1983, Fig. 1).
Starting from some initial configuration (choice of “0” or “1” states for all neurons) and assuming a fixed set of weights, the network can be run so as to minimize its potential energy by choosing states for each unit based on the states of its neighbors plus any external input, via the sigmoid function. Neurons receiving large negative (inhibitory) input minimize the potential energy when turned “off”, and those receiving large positive input minimize it when firing, as is reflected in the energy equation for the network (Hinton and Sejnowski 1983, Eq. (1)). Significant membrane potentials are local non-equilibrium states, so repeatedly choosing states for the units using the activation function simulates (in a very coarse-grained way) the brain’s settling into thermodynamic equilibrium, at least insofar as this process depends on neural spiking activity. If external input is added, the network can simulate the impact of the absorption of sensory signals on this process.
Hinton & Sejnowski propose a simple interpretation of such a network as a representation of the source of its external input signals: the state of each unit is interpreted as the truth-value assigned to a proposition, and the probability of a unit’s being in the “True” or “1” state at a given moment corresponds to the probability the system assigns to the corresponding proposition at that moment (“probabilities are represented by probabilities” (p. 448)). The “input” nodes correspond to pieces of sensory evidence, and the rest correspond to hypotheses invoked to explain the evidence. Except for the input units, whose states are overwhelmingly determined by the external information source, the probability of each unit (and thus each hypothesis) depends only on the states of the other units (hypotheses) plus the strength and sign of the connections between them. The network can thus represent complex probabilistic dependencies among hypotheses.
Given this interpretation of the units, the process of updating each unit’s state is equivalent to Bayesian inference.19 Bayes’s rule, written in terms of the natural exponential function and the log prior and likelihood ratios, is identical in form to the sigmoid activation function, where the prior ratio for H is implemented by unit h’s threshold term and the likelihood ratio of H given E is implemented by the symmetrical weight between h and e.20
(a)
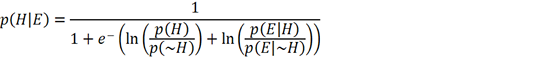
(b)
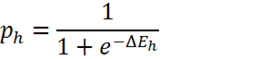
(c)
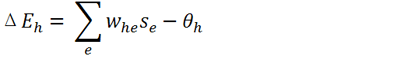
(d)
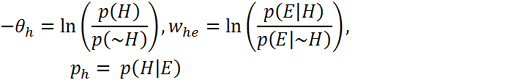
Figure 3. Equations adapted from Hinton and Sejnowski 1983. (a) Bayes’s rule, expressed in terms of the natural exponential function. (b) The sigmoid activation function used in Hinton & Sejnowski’s network (with temperature parameter T omitted), where ph is the probability of unit h firing, i.e. being in the “True” state and ΔEh is the difference between the energy of the network with unit h in the “False” state and the energy with h in the “True” state. (c) ΔEh is determined locally for each unit by its weighted, summed input minus its threshold term, where whe is the symmetrical weight between unit h and unit e, se is the binary state of unit e, and θh is the threshold for unit h (the term for direct external input is omitted here for simplicity). (d) Interpreting variables in the model as representing relevant probabilities yields a formal equivalence between energy minimization in the network and statistical inference using Bayes’s rule. The weights and biases of the network are interpreted as log probability ratios, while the probability of unit h being “on” is interpreted as the probability assigned to hypothesis H.
Since the network’s settling into equilibrium can thus be interpreted as massively parallel Bayesian inference, the potential energy of a global state is a measure of the incoherence of the corresponding collection of hypotheses. As Hinton & Sejnowski put it, “The energy of a state can.be interpreted as the extent to which a combination of hypotheses fails to fit the input data and violates the constraints between hypotheses, so in minimizing energy the system is maximizing the extent to which a perceptual interpretation fits the data and satisfies the constraints” (p. 449).
Obviously, there is no reason to suppose that an arbitrary collection of weights will result in a very coherent set of hypotheses. Learning can be accomplished in the network by adjusting the weights so as to minimize the difference between the network’s equilibrium states when running independently of external input and its equilibrium states given fixed external input (p. 452). This amounts to fitting a generative model to the data supplied at the input nodes. By supplying sustained input and letting the network settle into equilibrium, the generative model is implicitly inverted.
Since nothing about the content of the units has been assumed beyond bare truth-evaluability, this model supplies a purely formal theory of inductive inference of a different kind than the logical models discussed earlier: rather than appealing to the internal syntax of language-like representations to explain inference, this model appeals to a structurally specifiable notion of coherence, which can be shown to increase as representations are updated. In this respect, it thus realizes Harman’s account of inductive inference.
As in Harman’s account, the model subsumes confirmation holism as a special case of the holism of inferential processes, since fitting the data is treated as a special case of coherence.21 Just as observations are in practice accorded proportionally more weight than theoretical assumptions in determining posterior belief, it may be supposed that the incoming sensory signal is generally stronger and more consistent than endogenously generated signals in neural networks like the one discussed here, so that in practice coherence can only be achieved along with empirical adequacy.
There is a loose end concerning acceptances. It was suggested earlier that the same holistic process that results in rational change of belief could result in rational change in acceptance. There are many ways in which one might implement this possibility in the sort of model just discussed, but perhaps the simplest is to suppose that hypothetical reasoning makes use of the same representational vehicles that subserve occurrent and dispositional beliefs.
The longer-term knowledge underlying inferential transitions, encoded in synaptic weights, can remain the same in both processes. Entertaining a hypothesis may be a matter of subtly modulating the activity of the units corresponding to occurrent beliefs, which may be supposed to spread activation through the network in a pattern similar to (but perhaps weaker than) one that would occur were one fully committed to the inference. Predictive processing models (as well as a wealth of empirical evidence independent of them) predict in any case that the same neural hardware is used both for perceptual representation and (possibly concurrent) mental imagery. The simultaneous representation of what is believed and what is provisionally accepted may be seen as a generalization of this process to amodal representations.
The model just discussed provides a particularly perspicuous, but highly idealized and abstract, account of the neural implementation of Bayesian inference. Similar mechanisms exist in more sophisticated models, including predictive processing models. For brevity, I’ll consider two models with respect to their differences from the one just discussed, and argue that they implement inference in similar ways.
The Helmholtz machine, a model of perception proposed by Hinton, Dayan , Frey & Neal (Hinton et al. 1995), is in some ways an intermediary between the one just considered and predictive processing models. It uses binary stochastic units arranged into layers: an input layer whose states are determined externally and a series of hidden layers. The units in each layer are connected to those in the layer above by “recognition” weights, and to those in the layer below by distinct “generative” weights. These sets of weights (plus biases) implement the corresponding recognition and generative models. Like predictive coding models, this model incorporates hierarchy.
Since the Helmholtz machine encodes a feedforward recognition model in its bottom-up weights, perceptual inference does not require letting the system settle to equilibrium to invert the generative model, but nor does it employ top-down priors dynamically, so it arguably does not implement true coherence-maximizing inference in Harman’s sense. Still, the weights can be learned by a process of implicit error minimization, in which the states of the units under the generative and recognition models are used as targets to train one another (Frey et al. 1997, p. 5). This learning process increases the coherence of the sets of representations induced by perceptual input. The creators of the model acknowledge that the lack of a role for top-down influence during perception limits its biological plausibility (while increasing recognition speed) (Frey et al. 1997, p. 21).
The predictive processing model described by Friston (Friston 2005) differs from the Helmholtz machine in at least two major respects: (a) it employs the signature mechanism of online predictive coding, whereby only the difference between top-down predictions and bottom-up error signals is passed up the hierarchy, and (b) it does this by including dedicated nodes that represent prediction errors, as well as recurrent and lateral connections that explicitly encode the variances of the prediction errors.
This model seems to differ markedly from the others in that its nodes represent the magnitudes of environmental quantities and prediction errors rather than binary propositions. This difference may be important in various ways but I argue presently that it does not affect the truth-preserving character and thus the inferential status of the transitions in the model. The difference concerns only what is explicitly encoded, rather than the truth-evaluability of the model’s representations.
Bayesian inference in its most general form takes arbitrary probability distributions22 as inputs and yields a posterior distribution as output. The common use of Bayes’s theorem to update the posterior probability of hypothesis H given evidence E can be assimilated to the more general case by noting that the relevant probabilities yield a Bernoulli distribution over Boolean truth-values of the claims E and H. In the other direction, a distribution over values of a real-valued variable can be thought of as an assignment of probability to each of a range of hypotheses about the value of that variable.23 Thus, Bayesian inference in general satisfies the truth-evaluability constraint on inferential processes.
It remains to be seen exactly why we should expect transitions in the more complicated models to preserve truth (and more specifically, to conform at least approximately to Bayesian norms). First, since inference in a hierarchical generative model depends on many coordinated (layers of) nodes, improvement of the generative model guarantees increased coherence among the hypotheses it represents. Second, these models can be understood as variations on the simpler proposal discussed earlier by appeal to their common denominator: the idea that minimization of potential energy is equivalent to improvement of a generative model of the external source(s) of the system’s input. The main differences between the models in this respect concern how they represent the distributions that constitute the model.
In brief, the generative distribution in both the Hopfield-inspired model and the Helmholtz machine are encoded in the synaptic weights (plus biases) and activities of the units, since the probability of each unit firing (and therefore the probability assigned to the represented proposition) is determined directly by its weighted, summed input, which also defines the unit’s contribution to the energy function for the network. In the latter model, the Helmholtz free energy measures the potential energy of the system in various states, and the two distinct sets of weights make different contributions to this term.24
Predictive processing models such as Friston’s, as Bogacz 2015 shows, minimize the free energy by adjusting the explicitly represented model parameters (mean and variance) used to define the relevant distributions. As has been widely discussed (see e.g. Clark 2013 and Hohwy 2013, ch. 3), the precision (i.e. inverse variance) of the error units in such models is used to adjust the relative influence of priors and incoming evidence at various levels of hierarchy, so that the posterior means (which implement the inferred hypotheses) are a precision-weighted combination of the prior and likelihood. These models thus in effect use the precision as a way of controlling the tradeoff between the two criteria in Harman’s account of induction (conservatism and coherence).25
Importantly, this precision-weighting is not a special feature of predictive coding models but falls naturally out of Bayesian inference. Relatedly, as Arnold Zellner (Zellner 1988) shows, Bayes’s theorem itself mandates as much conservatism as possible with respect to the total amount of information in the input VS the output of a process. It is an optimal information-processing rule in that it maximally conserves information, subject to the constraint that it produce a probability distribution.26
In summary, I’ve argued that there is no distinctive sense of ‘inference’ that covers all uncontroversial, commonsense uses of the term but fails to cover perceptual inference as characterized by Helmholtzian theories. In the process, I’ve defended Harman’s (Harman 1973) view of inference as coherence-seeking, conservative change in view, as well as a simple descriptive conception of rationality as the tendency to preserve truth in the transitions between one’s internal representations. I also argued in some detail that Helmholtzian models of perception implement inference so described. If these models are accurate as rough descriptions of biological cortical networks, and if Harman’s conception of inductive inference is defensible, Helmholtz’s theory that perception is a form of inference is vindicated.
I close by addressing the extremely general applicability of the Bayesian perspective defended above, which one might fear borders on triviality. Since I’ve claimed in effect that any system of interdependent variables can be interpreted as a set of propositions, it may be difficult to imagine any regular mental or neural process that would not count as inference.
However, the conception of inference on offer here is in the end only as trivial as is the truth-evaluability of the representations over which it is defined. I have suggested that all content is in effect truth-evaluable, and rejected a popular view about what it takes to be a truth-bearer (namely, internal compositional structure), but next to nothing has been said about the determinants of content in this paper, beyond a nod to the notion of structural representation appealed to by predictive processing theorists. That account of representation does not seem to trivialize it, and may even rule out simple feedforward systems as involving genuine representation and therefore genuine inference.27
The most radical conclusion one might draw from the line of argument developed here is that sensory representations are to be counted, somehow, among the propositional attitudes. This may seem to strain ordinary usage, but as in the case of inference, a principled claim that a term such as “belief” is being used in an extended sense requires substantive support. Commonsense psychology implicitly defines propositional attitudes in terms of their functional roles, but does not determine a priori which representations will turn out to play those roles, and many considerations suggest that representations throughout perceptual and cognitive processing hierarchies function similarly. This is not to say that there are no important differences among such representations. It was conceded above, for example, that the contents of sensory representations are difficult to spell out convincingly. I should also stress that while I see no pressing theoretical need to suppose that Helmholtzian systems exhibit modularity, this is ultimately an empirical question, and the argument here requires only that perceptual inference itself not be encapsulated, not that such systems are in no way modular.
A final reply to worries about triviality touches on a point of philosophical methodology. We are sometimes concerned to preserve the interest of debates by avoiding interpretations of key concepts that render them too broadly applicable, but I am not sure that this avoidance is always desirable. If a relatively deflationary conception of inference is sufficient to capture the uncontroversial features of the commonsense notion, as well as to serve the needs of Bayesian theories in cognitive science (and Helmholtzian theories of perception in particular), it’s not clear a priori why we should want a more discriminating account. Important generalizations about inference over syntactically structured representations, or conscious, deliberate reasoning, can be captured by specific accounts of those phenomena. A clear conception of the more basic notion of inference can only assist in these endeavors.
References
Aggelopoulos, N. C. (2015). Perceptual inference. Neuroscience & Biobehavioral Reviews, 55, 375-392.
Anderson, J. R. (1991). Is human cognition adaptive? Behavioral and Brain Sciences, 14, 471-517.
Bogacz, R. (2015). A tutorial on the free-energy framework for modelling perception and learning. Journal of Mathematical Psychology. http://dx.doi.org/10.1016/j.jmp.2015.11.003.
Boghossian, P. (2014). What is inference? Philosophical Studies, 169 (1), 1-18.
BonJour, L. (1985). The structure of empirical knowledge. Cambridge: Harvard University Press.
Broome, J. (2014). Comments on Boghossian. Philosophical Studies, 169 (1), 19-25.
Burge, T. (2010). Origins of objectivity. Oxford: Oxford University Press.
Carnap, R. (1950). Logical foundations of probability. Chicago: University of Chicago Press.
Clark, A. (2013). Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behavioral & Brain Sciences, 36 (3), 181-204.
Davidson, D. (1986). A coherence theory of truth and knowledge. In E. LePore (Ed.) Truth and interpretation: Perspectives on the philosophy of Donald Davidson. Oxford: Basil Blackwell.
Dennett, D. C. (1978). Brainstorms. Cambridge: MIT Press.
Drayson, Z. (2012). The uses and abuses of the personal/subpersonal distinction. Philosophical Perspectives, 26 (1), 1-18.
——— (2017). Modularity and the predictive mind. In T. Metzinger & W. Wiese (Eds.) Philosophy and predictive processing. Frankfurt am Main: MIND Group.
Dretske, F. (1981). Knowledge and the flow of information. Cambridge: MIT Press.
Evans, G. (1982). The varieties of reference. Oxford: Oxford University Press.
Fodor, J. A. (1975). The language of thought. Cambridge: Harvard University Press.
——— (1983). The modularity of mind: An essay on faculty psychology. Cambridge: MIT Press.
——— (2007). The revenge of the given. In B.P. McLaughlin & J.D. Cohen (Eds.) Contemporary debates in philosophy of mind. Malden: Blackwell.
Frey, B. J., Dayan, P. & Hinton, G. E. (1997). A simple algorithm that discovers efficient perceptual codes. In M. Jenkin & L.R. Harris (Eds.) Computational and biological mechanisms of visual coding. New York: Cambridge University Press.
Friston, K. (2005). A theory of cortical responses. Phil. Trans. R. Soc. B, 360, 815-836. http://dx.doi.org/10.1098/rstb.2005.1622.
——— (2011). Action understanding and active inference. Biological Cybernetics, 104, 137-160.
Goldstein, D. G. & Gigerenzer, G. (2002). Models of ecological rationality: The recognition heuristic. Psychological Review, 109 (1), 75-90.
Gładziejewski, P. (2015). Predictive coding and representationalism. Synthese, 1-24. https://dx.doi.org/10.1007/s11229-015-0762-9.
Harman, G. (1973). Thought. Princeton: Princeton University Press.
——— (1986). Change in view: Principles of reasoning. Cambridge: MIT Press.
Harrison, L. M., Stephan, K. E., Rees, G. & Friston, K. J. (2007). Extra-classical receptive field effects measured in striate cortex with fMRI. NeuroImage, 34 (3), 1199-1208. http://dx.doi.org/10.1016/j.neuroimage.2006.10.017.
Hinton, G. E. (2007). Learning multiple layers of representation. Trends in Cognitive Sciences, 11 (10), 428-434. https://dx.doi.org/10.1016/j.tics.2007.09.004.
Hinton, G. E. & Sejnowski, T. J. (1983). Optimal Perceptual Inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.
Hinton, G. E. & Zemel, R. (1994). Autoencoders, minimum description length and Helmholtz free energy. Advances in Neural Information Processing Systems, 6, 3-10.
Hinton, G. E., Dayan, P., Frey, B. J. & Neal, R. (1995). The wake-sleep algorithm for unsupervised neural networks. Science, 268, 1158-1161.
Hohwy, J. (2013). The predictive mind. Oxford: Oxford University Press.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences USA, 79, 2554-2558.
Huang, Y. & Rao, R. P. N. (2011). Predictive coding. Wiley Interdisciplinary Reviews: Cognitive Science, n/a-n/a. https://dx.doi.org/10.1002/wcs.142.
Jenkin, Z. & Siegel, S. (2015). Cognitive penetrability: Modularity, epistemology, and ethics. Review of Philosophy and Psychology, 6 (4), 531-545. https://dx.doi.org/10.1007/s13164-015-0252-5.
Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. (1983). Optimization by simulated annealing. Science, New Series, 220 (4598), 671-680.
Kyburg, H. E. Jr. (1961). Probability and the logic of rational belief. Middletown: Wesleyan University Press.
Lehrer, K. (1986). The coherence theory of knowledge. Philosophical Topics, 14, 5-25.
Lupyan, G. (2015). Cognitive penetrability of perception in the age of prediction: Predictive systems are penetrable systems. Review of Philosophy and Psychology, 6 (4), 547-569. https://dx.doi.org/10.1007/s13164-015-0253-4.
Mandelbaum, E. (2016). Attitude, inference, association: On the propositional structure of implicit bias. Noûs, 50 (3), 629–658. https://dx.doi.org/10.1111/nous.12089.
Newen, A., Marchi, F. & Brössel, P. (2017). Consciousness and Cognition (47): S.I. Cognitive penetration and predictive coding (pp. 1-112). http://www.sciencedirect.com/science/journal/10538100/47.
O'Callaghan, C., Kveraga, K., Shine, J. M., Adams, Jr. & Bar, M. (2017). Predictions penetrate perception: Converging insights from brain, behaviour and disorder. Consciousness and Cognition, 47, 63–74. https://dx.doi.org/10.1016/j.concog.2016.05.003.
Oh, J. & Seung, H. S. (1997). Learning generative models with the up-propagation algorithm. NIPS 1997.
Orlandi, N. (2015). Bayesian perception is ecological perception. http://mindsonline.philosophyofbrains.com/2015/
session2/bayesian-perception-is-ecological-perception/.
Pearl, J. (1988). Probabilistic reasoning in intelligent systems: Networks of plausible inference. San Francisco: Morgan Kaufman Publishers, Inc.
Quilty-Dunn, J. (unpublished). Phenomenal contrast and perceptual belief.
Quine, W. V. (1951). Two dogmas of empiricism. The Philosophical Review, 60 (1), 20-43. http://www.jstor.org/stable/2181906.
Rao, R. P. N. & Sejnowski, T. J. (2002). Predictive coding, cortical feedback, and spike-timing-dependent plasticity. In R. P. Rao, B. A. Olshausen & M. S. Lewicki (Eds.) Probabilistic models of the brain: Perception and neural function. Cambridge: MIT Press.
Reichenbach, H. (1949). The theory of probability: An inquiry into the logical and mathematical foundations of the calculus of probability. Berkeley: University of California Press.
Rosenthal, D. M. (2005). Consciousness and mind. Oxford: Clarendon Press.
Searle, J. (1983). Intentionality: An essay in the philosophy of mind. New York: Cambridge University Press.
Siegel, S. (2010). The contents of visual experience. Oxford: Oxford University Press.
Stich, S. P. (1978). Beliefs and subdoxastic states. Philosophy of Science, 45 (4), 499-518.
Tye, M. (1991). The imagery debate. Cambridge: MIT Press.
Von Helmholtz, H. (1860/1962). Treatise on physiological optics. New York: Dover.
Wright, C. (2014). Comment on Paul Boghossian, ‘What is inference’. Philosophical Studies, 169, 27-37.
Zellner, A. (1988). Optimal information processing and Bayes‘s theorem. The American Statistician, 42 (4), 278-280.
1 By ‘model’ I mean a formal structure along with its interpretation, which I take to be a type of theory.
2 By ‘acceptance’ I mean, like Wright , an attitude toward a proposition that, like belief, involves commitment, but in which the commitment may be merely provisional, hypothetical, or temporary. Thus, as Wright claims (Wright 2014, p. 29), supposition is a kind of acceptance—as is belief.
3 The lottery paradox, invented by Henry Kyburg (Kyburg 1961 p. 197) and often discussed in the context of epistemology, arises if one accepts a principle to the effect that any very highly probable hypothesis should be accepted as true. In a large lottery with one winner, “Ticket number X will lose” is extremely probable for each X. Thus, given such a principle, we should accept that no ticket will win, which contradicts the prior belief that one ticket will win.
4 Harman offers one more reason to accept a holistic account of inference: arguably, one may not rationally infer that P without also believing that there is no evidence against P of which one is ignorant. To respect this principle while avoiding a regress of inferences, we must suppose that the belief that there is no undermining evidence against P, call it ~UE(P), is inferred along with P (as part of a total most explanatory account) rather than antecedently, since inference to ~UE(P) would itself require a similar belief ~UE(~UE(P)), which would require a previous inference, etc. (Harman 1973, p. 153). I mention this argument only in a footnote, because it depends on many assumptions tangential to the topic at hand.
5 Practical rationality will not be discussed here, but the notion of “active inference” (Friston 2011) suggests that a unification of theoretical and practical reason is also conceivable along these lines, since active inference makes transitions between high-level hypotheses and sensory predictions truth-preserving and is thus a rational process in the sense defined here.
6 I thank an anonymous reviewer for suggesting this connection to Gigerenzer’s work. In the bigger picture, of course, there is potentially some tension between that work and the Bayesian perspective afforded by predictive processing theories (though one may consider approximate Bayesian inference a heuristic of sorts).
7 Thanks to Wanja Wiese for suggesting this connection to Anderson’s work on the method of “rational analysis” (Anderson 1991).
8 To anticipate a bit, it may be objected that the automatic inference supposed by Helmholtz to occur unconsciously is certainly not goal-oriented behavior. But this depends on how one defines the latter notion. Perception is arguably often goal-oriented. And an inference may seem to be ‘automatic’ because it is drawn immediately in the face of compelling evidence, as may be the case with the sensory evidence involved in perceptual inference.
9 Active inference may provide a route to making sense of this, since predictions include intentions, motor commands, and other representations with a “world-to-mind” direction of fit. Another possibility would be to construe any action as constitutively involving an intention-in-action (along the lines of Searle 1983), whose content represents the satisfaction-condition of a desire and is true when the action succeeds.
10 In making the point about symmetry, Mandelbaum is discussing what distinguishes associative structures in memory from propositional structures, not what distinguishes associative from non-associative transitions. But he also claims (reasonably, I think) that the only difference between associative structures and transitions is that the former involve co-activation of representations while the latter involve one representation activating another after some delay.
11 This issue is somewhat complicated in the context of Mandelbaum’s discussion. On the one hand, he treats it as sufficient for association that one concept activate a second without a further mediating computational relation (p. 10), and this description would be satisfied by a one-way synaptic connection between two neural representational vehicles of the appropriate sort. On the other hand, he distinguishes between (a) associative connections between mental states and (b) associative neural network “implementation bases” for such states. But the latter distinction, if read as a dichotomy, would beg the question against those who take connectionist models to be both models of neural dynamics and theories of mental architecture, as I in effect do.
12 One could still suppose in this case that perception involved inference at some later stage of processing, perhaps in some sub-perceptual module. I argue that the inputs to perception are truth-apt so I do not explore this possibility here.
13 Burge (Burge 2010, pp. 230-232) argues in effect that any truth-evaluable representation, at least of the kind involved in perception, must be structured in a way that both allows for repeated application (i.e. exhibits generality) and depends on particulars in a specific context of application. This suggests object-property structure in the semantics, but Burge does not discuss syntactic structure, and allows that the particular element in perceptual representation may be “entirely implicit”.
15 As Zoe Drayson points out, the use of the term “subpersonal” to type-individuate psychological states marks a perhaps dubious extension of its original use to distinguish among types of psychological explanation (Drayson 2012, section 2.5; see also Dennett 1978). I intend the term to pick out states or representations that occur within special-purpose cognitive subsystems or modules, in accordance with contemporary usage, and, as Drayson points out, with Stephen Stich’s use of the term “subdoxastic” (Stich 1978), discussed below.
16 Perceptual processing may occur within a cognitive subsystem but still realize Harman’s account of inference at the “subpersonal” level, in that coherence is maximized with respect to representations within the module. Such processing would fail to meet the Boghossian/Wright conditions on inference discussed in section 2.3, however, because the “inferences” in question would not be attributable to the subject capable of paradigm (e.g. conscious, deliberate) reasoning.
17 Drayson is equivocal, however, about whether this highly contingent, possibly transient form of encapsulation suffices for modularity as traditionally understood (p. 10). Conditional independencies between layers in a Bayesian network can be precisely characterized using the concept of a Markov blanket (Pearl 1988, p. 97, 121), but this form of independence does not seem to amount to information encapsulation in Fodor’s sense (Fodor 1983), since as Drayson mentions, “modules” defined in such a way may overlap.
18 This distinction may correspond to that between rapidly changing occurrent representations encoded in neural activities and those encoded in synaptic weight matrices, which implicitly represent regularities over longer time-scales. It is to be expected that the latter contents would not be immediately accessible to consciousness.
19 Historically, ideas from statistical mechanics were applied to optimization problems on the basis of an analogy between the behavior of physical systems with large numbers of interacting parts and functions with large numbers of interacting variables (Kirkpatrick et al. 1983). The argument pursued here proposes a more direct link between energy minimization and Bayesian inference, exploiting the idea that the mind/brain realizes a complex statistical model in virtue of its complex physical structure.
20 This is a simplified formulation, which ignores direct external input as well as the temperature parameter in the sigmoid function, which is assumed to be set to 1. See Hinton and Sejnowski 1983, Eqs. (2), (3) and (5) and discussion. Note that the sum of weighted input in Fig.3(c) corresponds to using Bayes’s rule to update the probability of H given multiple pieces of independent evidence.
The authors point out two important issues with this implementation of Bayesian inference: (a) symmetrical weights are required if each unit is to implement inference using only local information, but the relation between evidence and hypothesis described by Bayes’s theorem is not symmetrical, and (b) the weights and thresholds must be so designed as to capture the effect of the negation of the evidence on a hypothesis. These issues are surmountable, but I omit the details here (see pp. 450-451 & 453 of the paper).
21 I thank an anonymous reviewer for pressing me to emphasize this point.
22 Since I take the difference between continuous and discrete distributions not to affect the main argument here, I use ‘distribution’ throughout, without meaning to exclude distributions that could only be characterized using a density function.
23 One could interpret a continuous distribution in terms of an infinite range of hypotheses, but in this case the probability assigned to each individual hypothesis would be 0. This is not very useful, but the distribution can be described meaningfully and as precisely as one likes by specifying a set of hypotheses each of which covers an arbitrarily small range of values.
24 This is reflected in equations (3) and (5) in Hinton et al. 1995, which define the cost functions for learning. See Hinton and Zemel 1994 for a general discussion of the connection between Helmholtz free energy and generative models.
25 I owe this point to an anonymous reviewer.
26 Thanks to Wanja Wiese for bringing this point, and the relevant reference, to my attention.
27 Since structural homomorphism comes in degrees, it may be doubted whether even representation (so construed) can provide an ironclad criterion for distinguishing inference from simpler mechanisms, or more broadly, minds from non-minds. Perhaps this distinction can be drawn, if at all, by appeal to the sorts of interesting (and increasingly abstract) contents that more complex systems with deeper hierarchies can represent.